题目内容
设集合A满足:若a∈A,a≠1,则
∈A,已知2∈A,则符合集合A的条件的是( )
| 1 |
| 1-a |
A、{-1,
| ||
| B、{-1,2} | ||
C、{-1,
| ||
D、{
|
考点:元素与集合关系的判断
专题:集合
分析:抓住条件:若a∈A,a≠1,则
∈A,由2∈A推导-1∈A,则排除C,D,剩下A,B,对
进行思考,发现-1也要符合条件:若a∈A,a≠1,则
∈A,此时即可得出答案.
| 1 |
| 1-a |
| 1 |
| 2 |
| 1 |
| 1-a |
解答:
解;∵2∈A,∴
∈A,即-1∈A,
又∵-1∈A,
∴
∈A,即
∈A,
∴A中必有元素2,-1,
,
故选:A.
| 1 |
| 1-2 |
又∵-1∈A,
∴
| 1 |
| 1-(-1) |
| 1 |
| 2 |
∴A中必有元素2,-1,
| 1 |
| 2 |
故选:A.
点评:本题考查元素与集合的关系,易错点在元素
,利用排除法时,要对其进行思考,不可轻下判断
| 1 |
| 2 |

练习册系列答案
相关题目
在△ABC中,已知sin2A+sin2B+sin2C=2,则△ABC为( )
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
“m<8”是“方程
-
=1表示双曲线”的( )
| x2 |
| m-10 |
| y2 |
| m-8 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
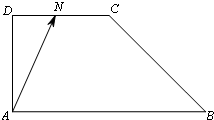 如图,在梯形ABCD中,AB∥DC,AD⊥AB,AD=DC=
如图,在梯形ABCD中,AB∥DC,AD⊥AB,AD=DC=