题目内容
“m＜8”是“方程
-
=1表示双曲线”的（ ）
| x2 |
| m-10 |
| y2 |
| m-8 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：圆锥曲线的定义、性质与方程,简易逻辑
分析：根据双曲线的定义以及充分条件和必要条件的定义进行判断即可得到结论．
解答：
解：若方程
-
=1表示双曲线，
则（m-10）（m-8）＞0，即m＞10或m＜8．
∴“m＜8”是“方程
-
=1表示双曲线”的充分而不必要条件，
故选：A．
| x2 |
| m-10 |
| y2 |
| m-8 |
则（m-10）（m-8）＞0，即m＞10或m＜8．
∴“m＜8”是“方程
| x2 |
| m-10 |
| y2 |
| m-8 |
故选：A．
点评：本题主要考查充分条件和必要条件的判断，利用双曲线的定义求出m的取值范围是解决本题的关键，比较基础．
练习册系列答案
相关题目
设集合A满足：若a∈A，a≠1，则
∈A，已知2∈A，则符合集合A的条件的是（ ）
| 1 |
| 1-a |
A、{-1，
| ||
| B、{-1，2} | ||
C、{-1，
| ||
D、{
|
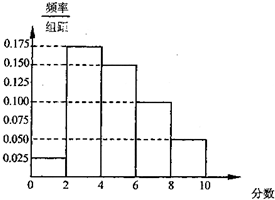某个团购网站为了更好地满足消费者需求，对在其网站发布的团购产品展开了用户调查，每个用户在使用了团购产品后可以对该产品进行打分，最高分是10分．上个月该网站共卖出了100份团购产品，所有用户打分的平均分作为该产品的参考分值，将这些产品按照得分分成以下几组：第一组[0，2），第二组[2，4），第三组[4，6），第四组[6，8），第五组[8，10]，得到的频率分布直方图如图所示．