题目内容
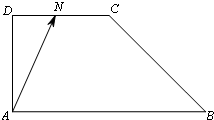如图，在梯形ABCD中，AB∥DC，AD⊥AB，AD=DC=| 1 |
| 2 |
| AN |
| AB |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：以AB、AD所在直线分别为x、y，建立如图坐标系，求出相关点的坐标，即可求解
•
的表达式，确定最大值．
| AN |
| AB |
解答：
解：以AB、AD所在直线分别为x、y，建立如图坐标系，可得
A（0，0），B（4，0），C（2，2），D（0，2）
N坐标为（x，2），（x∈[0，2]），
•
=（x，2）（4，0）=8x+2∈[2，8]．
则
•
的最大值为：8．
故答案为：8．
解：以AB、AD所在直线分别为x、y，建立如图坐标系，可得A（0，0），B（4，0），C（2，2），D（0，2）
N坐标为（x，2），（x∈[0，2]），
| AN |
| AB |
则
| AN |
| AB |
故答案为：8．
点评：本题在一个直角三角形中求向量数量积的最大值，着重考查了直角梯形的性质、平面向量数量积的坐标运算等知识，属于中档题．
练习册系列答案
相关题目
设集合A满足：若a∈A，a≠1，则
∈A，已知2∈A，则符合集合A的条件的是（ ）
| 1 |
| 1-a |
A、{-1，
| ||
| B、{-1，2} | ||
C、{-1，
| ||
D、{
|