题目内容
已知数列{an}满足：a1=m（m≠1），an+1=2an+3n-1．
（1）设bn=
，求数列{bn}的通项公式；
（2）在（1）的条件下，若对任意的正整数n，都有an+1≥an，求实数m最小的可能取值．
（1）设bn=
| an+1 |
| 3n |
（2）在（1）的条件下，若对任意的正整数n，都有an+1≥an，求实数m最小的可能取值．
考点：数列递推式
专题：综合题,点列、递归数列与数学归纳法
分析：（1）由题意an+1=2an+3n-1，得：an+1-3n=2（an-3n-1），所以数列{an-3n-1}是首项为m-1，公比为2的等比数列，进而求出an，即可求数列{bn}的通项公式；
（2）由对任意的正整数n，都有an+1≥an，可得m≥-2•(
)n-1+1，利用函数的单调性，即可得出结论．
（2）由对任意的正整数n，都有an+1≥an，可得m≥-2•(
| 3 |
| 2 |
解答：
解：（1）由题意an+1=2an+3n-1，
得：an+1-3n=2（an-3n-1），
∴数列{an-3n-1}是首项为m-1，公比为2的等比数列．
∴an-3n-1=（m-1）•2n-1，
∴an=3n-1+（m-1）•2n-1，
∵bn=
，
∴bn=1+（m-1）•(
)n；
（2）∵对任意的正整数n，都有an+1≥an，
∴3n+（m-1）•2n≥3n-1+（m-1）•2n-1，
∴m≥-2•(
)n-1+1，
∵f（x）=-2•(
)x-1+1在R上单调递减，
∴m≥-2+1=-1，
∴实数m最小的可能取值为-1．
得：an+1-3n=2（an-3n-1），
∴数列{an-3n-1}是首项为m-1，公比为2的等比数列．
∴an-3n-1=（m-1）•2n-1，
∴an=3n-1+（m-1）•2n-1，
∵bn=
| an+1 |
| 3n |
∴bn=1+（m-1）•(
| 2 |
| 3 |
（2）∵对任意的正整数n，都有an+1≥an，
∴3n+（m-1）•2n≥3n-1+（m-1）•2n-1，
∴m≥-2•(
| 3 |
| 2 |
∵f（x）=-2•(
| 3 |
| 2 |
∴m≥-2+1=-1，
∴实数m最小的可能取值为-1．
点评：本题考查数列的通项，考查恒成立问题，考查等比数列的证明，正确构造数列是关键．
练习册系列答案
阅读快车系列答案
相关题目
设集合A满足：若a∈A，a≠1，则
∈A，已知2∈A，则符合集合A的条件的是（ ）
| 1 |
| 1-a |
A、{-1，
| ||
| B、{-1，2} | ||
C、{-1，
| ||
D、{
|
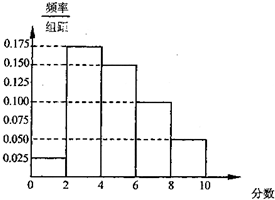某个团购网站为了更好地满足消费者需求，对在其网站发布的团购产品展开了用户调查，每个用户在使用了团购产品后可以对该产品进行打分，最高分是10分．上个月该网站共卖出了100份团购产品，所有用户打分的平均分作为该产品的参考分值，将这些产品按照得分分成以下几组：第一组[0，2），第二组[2，4），第三组[4，6），第四组[6，8），第五组[8，10]，得到的频率分布直方图如图所示．