题目内容
已知圆C经过A(5,2),B(3-
,2-
),且圆心C在直线x=3上.
(1)求圆C的方程;
(2)求过D(0,1)点且与圆C相切的两条切线方程.
| 2 |
| 2 |
(1)求圆C的方程;
(2)求过D(0,1)点且与圆C相切的两条切线方程.
考点:圆的切线方程,圆的一般方程
专题:综合题,直线与圆
分析:(1)解法1:利用圆心C在直线x=3上,设圆C的方程为(x-3)2+(y-b)2=R2,代入A,B的坐标,可得圆C的方程;解法2:圆心C在AB的垂直平分线l上,求出其方程,与直线x=3联立,求出圆心坐标,可得圆C的方程;
(2)当斜率不存在时,不存在经过D(0,1)的切线;解法1:切线方程为y=kx+1与圆的方程联立,利用方程有唯一一个解,可求切线方程;解法2:利用直线与圆相切,可得圆心C(3,2)到直线kx-y+1=0的距离等于圆的半径,可求切线方程.
(2)当斜率不存在时,不存在经过D(0,1)的切线;解法1:切线方程为y=kx+1与圆的方程联立,利用方程有唯一一个解,可求切线方程;解法2:利用直线与圆相切,可得圆心C(3,2)到直线kx-y+1=0的距离等于圆的半径,可求切线方程.
解答:
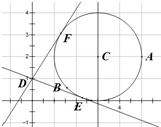 解:(1)解法1:∵圆心C在直线x=3上,
解:(1)解法1:∵圆心C在直线x=3上,
∴设圆C的方程为(x-3)2+(y-b)2=R2.
∵圆C经过A(5,2),B(3-
,2-
),
∴
,
∴
,∴解方程组得
,
∴设圆C的方程为(x-3)2+(y-2)2=4.
解法2:∵圆C经过A(5,2),B(3-
,2-
),
∴圆心C在AB的垂直平分线l上,且AB的中点坐标D(4-
,2-
).
∵kAB=
=
=
=
-1,∴kl=-(
+1).
∴直线l方程为y-(2-
)=-(
+1)(x-4+
).
∵圆心C在直线x=3上,∴y-(2-
)=-(
+1)(-1+
),
∴y=(
+1)(1-
)+2-
=2,∴圆心C(3,2),
∵R=
=2,∴圆C的方程为(x-3)2+(y-2)2=4.
(2)当斜率不存在时,不存在经过D(0,1)的切线;
解法1:当斜率存在时,设切线的斜率为k,则切线方程为y=kx+1.
解方程组
,
得(x-3)2+(kx-1)2=4,即(k2+1)x2-2(k+3)x+6=0.
∵方程有唯一一个解,∴△=4(k+3)2-4×6(k2+1)=0,∴5k2-6k-3=0,
∴解方程得k=
,∴切线方程y=
x+1.
解法2:∵直线与圆相切,∴圆心C(3,2)到直线kx-y+1=0的距离等于圆的半径,
∴d=r=
=2,∴
=2,∴4k2+4=9k2-6k+1,
∴5k2-6k-3=0,∴解方程得k=
,∴切线方程y=
x+1.
 解:(1)解法1:∵圆心C在直线x=3上,
解:(1)解法1:∵圆心C在直线x=3上,∴设圆C的方程为(x-3)2+(y-b)2=R2.
∵圆C经过A(5,2),B(3-
| 2 |
| 2 |
∴
|
∴
|
|
∴设圆C的方程为(x-3)2+(y-2)2=4.
解法2:∵圆C经过A(5,2),B(3-
| 2 |
| 2 |
∴圆心C在AB的垂直平分线l上,且AB的中点坐标D(4-
| ||
| 2 |
| ||
| 2 |
∵kAB=
| yA-yB |
| xA-xB |
2-(2-
| ||
5-(3-
|
| ||
2+
|
| 2 |
| 2 |
∴直线l方程为y-(2-
| ||
| 2 |
| 2 |
| ||
| 2 |
∵圆心C在直线x=3上,∴y-(2-
| ||
| 2 |
| 2 |
| ||
| 2 |
∴y=(
| 2 |
| ||
| 2 |
| ||
| 2 |
∵R=
| (5-3)2+(2-2)2 |
(2)当斜率不存在时,不存在经过D(0,1)的切线;
解法1:当斜率存在时,设切线的斜率为k,则切线方程为y=kx+1.
解方程组
|
得(x-3)2+(kx-1)2=4,即(k2+1)x2-2(k+3)x+6=0.
∵方程有唯一一个解,∴△=4(k+3)2-4×6(k2+1)=0,∴5k2-6k-3=0,
∴解方程得k=
3±2
| ||
| 5 |
3±2
| ||
| 5 |
解法2:∵直线与圆相切,∴圆心C(3,2)到直线kx-y+1=0的距离等于圆的半径,
∴d=r=
| |3k-2+1| | ||
|
| |3k-1| | ||
|
∴5k2-6k-3=0,∴解方程得k=
3±2
| ||
| 5 |
3±2
| ||
| 5 |
点评:本题考查圆的方程,考查直线与圆的位置关系,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知{an}是由正数组成的等比数列,Sn为其n项和.若a2a4=16,S3=7,则S4=( )
| A、15 | ||
| B、31 | ||
| C、63 | ||
D、
|
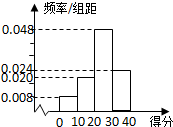 对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图,列出乙的得分统计表如下:
对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图,列出乙的得分统计表如下: 如图,在斜三棱柱ABC-A1B1C1中,点O是A1C1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.
如图,在斜三棱柱ABC-A1B1C1中,点O是A1C1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.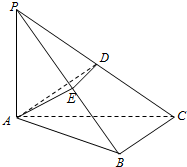 如图,在三棱锥P-ABC中,PA⊥平面ABC,AP=AB=2
如图,在三棱锥P-ABC中,PA⊥平面ABC,AP=AB=2