��Ŀ����
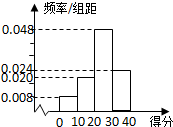 �Լס������������˶�Ա�ֱ���100�������еĵ÷��������ͳ�ƣ������ĵ÷�Ƶ�ʷֲ�ֱ��ͼ��ͼ���г��ҵĵ÷�ͳ�Ʊ����£�
�Լס������������˶�Ա�ֱ���100�������еĵ÷��������ͳ�ƣ������ĵ÷�Ƶ�ʷֲ�ֱ��ͼ��ͼ���г��ҵĵ÷�ͳ�Ʊ����£�| ��ֵ | [0��10�� | [10��20�� | [20��30�� | [30��40�� |
| ���� | 10 | 20 | 40 | 30 |
�����жϼס��������˶�Ա�ĸ��ɼ����ȶ��������۲�Ҫ��֤����
�������������е�100�������У��������и���ֵ����ij����ֲ����÷ֲ������ȡ��10���������ٴ���10�����������ѡ��2������һ������������2�������е÷ֲ�����30�ֵij���Ϊ�Σ���εķֲ��У�
���㣺��ɢ����������������뷽��,������������,�ŵ���ͼ�����ʼ��㹫ʽ
ר�⣺������ͳ��
�����������ɼĵ÷�Ƶ�ʷֲ�ֱ��ͼ���������һ�������е÷ֲ�����20�ֵĸ��ʣ�
���۲�ĵ÷�Ƶ�ʷֲ�ֱ��ͼ���ҵĵ÷�ͳ�Ʊ����õ��ijɼ����ȶ���
����������֪X��ȡֵΪ0��1��2���ֱ�������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��У�
���۲�ĵ÷�Ƶ�ʷֲ�ֱ��ͼ���ҵĵ÷�ͳ�Ʊ����õ��ijɼ����ȶ���
����������֪X��ȡֵΪ0��1��2���ֱ�������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��У�
���
�⣺�����ɼĵ÷�Ƶ�ʷֲ�ֱ��ͼ֪��
����һ�������е÷ֲ�����20�ֵĸ���p=��0.048+0.024����10=0.72������2�֣�
���۲�ĵ÷�Ƶ�ʷֲ�ֱ��ͼ���ҵĵ÷�ͳ�Ʊ���
�õ��ijɼ����ȶ�������5�֣�
�����շֲ����������[0��10����[10��20����[20��30����[30��40��
�ڳ���ı��������ֱ�Ϊ1��2��4��3������6�֣�
X��ȡֵΪ0��1��2������7�֣�
P(��=0)=
=
=
������9�֣�
P(��=1)=
=
=
������10�֣�
P(��=2)=
=
=
������11�֣�
��X�ķֲ���Ϊ��
����13�֣�
����һ�������е÷ֲ�����20�ֵĸ���p=��0.048+0.024����10=0.72������2�֣�
���۲�ĵ÷�Ƶ�ʷֲ�ֱ��ͼ���ҵĵ÷�ͳ�Ʊ���
�õ��ijɼ����ȶ�������5�֣�
�����շֲ����������[0��10����[10��20����[20��30����[30��40��
�ڳ���ı��������ֱ�Ϊ1��2��4��3������6�֣�
X��ȡֵΪ0��1��2������7�֣�
P(��=0)=
| ||
|
| 21 |
| 45 |
| 7 |
| 15 |
P(��=1)=
| ||||
|
| 21 |
| 45 |
| 7 |
| 15 |
P(��=2)=
| ||
|
| 3 |
| 45 |
| 1 |
| 15 |
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
���������⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ɢ����������ķֲ��е������е��⣬����ʱҪע���������֪ʶ�ĺ������ã�

��ϰ��ϵ�д�
 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
�����Ŀ
�Ķ���ͼ��ʾ�ij����ͼ��������Ӧ�ij��������sֵ���ڣ�������


| A��-3 | B��-21 | C��3 | D��21 |
��֪˫����C��
-
=1��a��0��b��0����������Ϊ2��A��BΪ�����Ҷ��㣬��PΪ˫����C�ڵ�һ��������һ�㣬��OΪ����ԭ�㣬��PA��PB��PO��б��Ϊk1��k2��k3����m=k1k2k3��ȡֵ��ΧΪ��������
| x2 |
| a2 |
| y2 |
| b2 |
A����0��3
| ||||
B����0��
| ||||
C����0��
| ||||
| D����0��8�� |
����A={x|2��x��4}��B={x|x��3}����A��B=��������
| A��[2��4�� |
| B��[3��+�ޣ� |
| C��[3��4�� |
| D��[2��3�� |
 ������ͼ��ʾ�ij����ͼ��������ʵ��x��ֵΪ-1ʱ������ĺ���ֵΪ2��������ʵ��x��ֵΪ3ʱ������ĺ���ֵΪ7��
������ͼ��ʾ�ij����ͼ��������ʵ��x��ֵΪ-1ʱ������ĺ���ֵΪ2��������ʵ��x��ֵΪ3ʱ������ĺ���ֵΪ7�� ��ͼ����Rt��AOB�У���OAB=
��ͼ����Rt��AOB�У���OAB=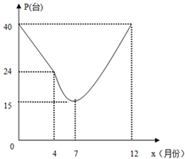 ���ڹ����ص���ֽ��ܻ�����ҵ��ij�ֽ��ܲ�Ʒ���г����ۻ�ů��ij�������������ֲ�Ʒ���������������ǩ��������ͬ��Լ��һ���ڽ���Ϊ0.1��Ԫ/̨��һ���ʵ����������P��̨�����´�x֮�������ͼ��ʾ������ϵ��4�µ�12�½��Ʒ��϶��κ�����ϵ����
���ڹ����ص���ֽ��ܻ�����ҵ��ij�ֽ��ܲ�Ʒ���г����ۻ�ů��ij�������������ֲ�Ʒ���������������ǩ��������ͬ��Լ��һ���ڽ���Ϊ0.1��Ԫ/̨��һ���ʵ����������P��̨�����´�x֮�������ͼ��ʾ������ϵ��4�µ�12�½��Ʒ��϶��κ�����ϵ����