题目内容
数列{an}前n项和Sn=
,数列{bn}满足3bn-bn-1=n(n≥2,n∈N*),
(1)求数列{an}的通项公式;
(2)求证:当b1≠
时,数列{bn-an}为等比数列;
(3)在题(2)的条件下,设数列{bn}的前n项和为Tn,若数列{Tn}中只有T3最小,求b1的取值范围.
| n2 |
| 4 |
(1)求数列{an}的通项公式;
(2)求证:当b1≠
| 1 |
| 4 |
(3)在题(2)的条件下,设数列{bn}的前n项和为Tn,若数列{Tn}中只有T3最小,求b1的取值范围.
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(1)由已知条件,利用公式an=
能求出数列{an}的通项公式.
(2)由已知条件3(bn-an)-(bn-1-an-1)=0,从而得到(bn-an)=
(bn-1-an-1),由此能证明{bn-an}是等比数列.
(3)由已知条件推导出bn=
+(b1-
)×(
)n-1,再由数列{Tn}中只有T3最小,能求出b1的取值范围.
|
(2)由已知条件3(bn-an)-(bn-1-an-1)=0,从而得到(bn-an)=
| 1 |
| 3 |
(3)由已知条件推导出bn=
| 2n-1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
解答:
(1)解:∵数列{an}前n项和Sn=
,
∴a1=S1=
,
an=Sn-Sn-1=
-
=
,
当n=1时,
=
=a1,
∴an=
,n∈N*.(4分)
(2)证明:∵数列{bn}满足3bn-bn-1=n(n≥2,n∈N*),
∴3(bn-an)-(bn-1-an-1)
=(3bn-bn-1)-3an+an-1=n-n=0,
∴(bn-an)=
(bn-1-an-1),且b1-a1≠0,
∴{bn-an}是以b1-a1为首项、
为公比的等比数列.(8分)
(3)解:∵{bn-an}是以b1-a1为首项、
为公比的等比数列,
∴bn=
+(b1-
)×(
)n-1,(10分)
∵数列{Tn}中只有T3最小,
∴
,解得-47<b1<-11,(13分)
此时,bn+1-bn=
-2×(b1-
)×(
)n>0,
于是,{bn}为递增数列,
∴n≤3时,bn<0,n≥4时bn>0,符合题意,
综上-47<b1<-11.(15分)
| n2 |
| 4 |
∴a1=S1=
| 1 |
| 4 |
an=Sn-Sn-1=
| n2 |
| 4 |
| (n-1)2 |
| 4 |
| 2n-1 |
| 4 |
当n=1时,
| 2n-1 |
| 4 |
| 1 |
| 4 |
∴an=
| 2n-1 |
| 4 |
(2)证明:∵数列{bn}满足3bn-bn-1=n(n≥2,n∈N*),
∴3(bn-an)-(bn-1-an-1)
=(3bn-bn-1)-3an+an-1=n-n=0,
∴(bn-an)=
| 1 |
| 3 |
∴{bn-an}是以b1-a1为首项、
| 1 |
| 3 |
(3)解:∵{bn-an}是以b1-a1为首项、
| 1 |
| 3 |
∴bn=
| 2n-1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
∵数列{Tn}中只有T3最小,
∴
|
此时,bn+1-bn=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
于是,{bn}为递增数列,
∴n≤3时,bn<0,n≥4时bn>0,符合题意,
综上-47<b1<-11.(15分)
点评:本题考查数列通项公式的求法,考查等比数列的证明,考查首项的取值范围的求法,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
相关题目
如图是一个几何体的三视图,则该几何体的体积是( )


| A、3 | ||
B、
| ||
| C、1 | ||
D、
|
 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB=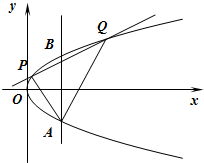 如图,两条相交线段AB、PQ的四个端点都在抛物线y2=x上,其中,直线AB的方程为x=m,直线PQ的方程为y=
如图,两条相交线段AB、PQ的四个端点都在抛物线y2=x上,其中,直线AB的方程为x=m,直线PQ的方程为y=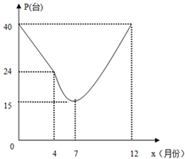 由于国家重点扶持节能环保产业,某种节能产品的市场销售回暖.某经销商销售这种产品,年初与生产厂家签订进货合同,约定一年内进价为0.1万元/台.一年后,实际月销售量P(台)与月次x之间存在如图所示函数关系(4月到12月近似符合二次函数关系).
由于国家重点扶持节能环保产业,某种节能产品的市场销售回暖.某经销商销售这种产品,年初与生产厂家签订进货合同,约定一年内进价为0.1万元/台.一年后,实际月销售量P(台)与月次x之间存在如图所示函数关系(4月到12月近似符合二次函数关系).