题目内容
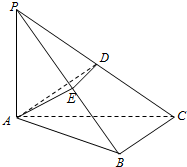 如图,在三棱锥P-ABC中,PA⊥平面ABC,AP=AB=2
如图,在三棱锥P-ABC中,PA⊥平面ABC,AP=AB=2| 3 |
(Ⅰ)证明:E为PB的中点;
(Ⅱ)若PB⊥AD,求直线AC与平面ADE所成角的正弦值.
考点:直线与平面所成的角
专题:空间角
分析:(Ⅰ)由已知条件推导出BC∥DE,再由D为PC中点,求出E为PB的中点.
(Ⅱ)由已知条件推导出平面PBC⊥平面ADE,从而得到BC⊥PB.过C作CH⊥ED于H,推导出∠CAH是直线AC与平面ADE所成的角.由此能求出直线AC与平面ADE所成角的正弦值.
(Ⅱ)由已知条件推导出平面PBC⊥平面ADE,从而得到BC⊥PB.过C作CH⊥ED于H,推导出∠CAH是直线AC与平面ADE所成的角.由此能求出直线AC与平面ADE所成角的正弦值.
解答:
 (Ⅰ)证明:∵BC∥平面ADE,BC?平面PBC,
(Ⅰ)证明:∵BC∥平面ADE,BC?平面PBC,
平面PBC∩平面ADE=DE,
∴BC∥DE.
∵D为PC中点,
∴E为PB的中点.
(Ⅱ)解:∵AP=AB,E为PB的中点,∴AE⊥PB,
又PB⊥AD,∴PB⊥平面ADE,
得DE⊥PB,且平面PBC⊥平面ADE.
由BC∥DE,得BC⊥PB.
过C作CH⊥ED于H,由平面PBC⊥平面ADE,∴CH⊥平面ADE.
∴∠CAH是直线AC与平面ADE所成的角.
∵BC∥DE,BC⊥PB,∴CH=BE=
PB=
,
∴sin∠CAH=
=
.
 (Ⅰ)证明:∵BC∥平面ADE,BC?平面PBC,
(Ⅰ)证明:∵BC∥平面ADE,BC?平面PBC,平面PBC∩平面ADE=DE,
∴BC∥DE.
∵D为PC中点,
∴E为PB的中点.
(Ⅱ)解:∵AP=AB,E为PB的中点,∴AE⊥PB,
又PB⊥AD,∴PB⊥平面ADE,
得DE⊥PB,且平面PBC⊥平面ADE.
由BC∥DE,得BC⊥PB.
过C作CH⊥ED于H,由平面PBC⊥平面ADE,∴CH⊥平面ADE.
∴∠CAH是直线AC与平面ADE所成的角.
∵BC∥DE,BC⊥PB,∴CH=BE=
| 1 |
| 2 |
| 6 |
∴sin∠CAH=
| CH |
| AC |
| ||
| 4 |
点评:本题考查线段中点的证明,考查直线与平面所成角的正弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
如图程序执行后输出的结果是S=( )


| A、3 | B、6 | C、10 | D、15 |
在如图所示的程序框图中,输入f0(x)=cosx,则输出的是( )
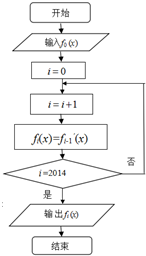

| A、sinx | B、-sinx |
| C、cosx | D、-cosx |
 运行如图所示的程序框图,当输入实数x的值为-1时,输出的函数值为2;当输入实数x的值为3时,输出的函数值为7.
运行如图所示的程序框图,当输入实数x的值为-1时,输出的函数值为2;当输入实数x的值为3时,输出的函数值为7.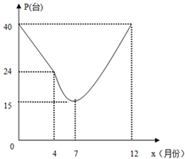 由于国家重点扶持节能环保产业,某种节能产品的市场销售回暖.某经销商销售这种产品,年初与生产厂家签订进货合同,约定一年内进价为0.1万元/台.一年后,实际月销售量P(台)与月次x之间存在如图所示函数关系(4月到12月近似符合二次函数关系).
由于国家重点扶持节能环保产业,某种节能产品的市场销售回暖.某经销商销售这种产品,年初与生产厂家签订进货合同,约定一年内进价为0.1万元/台.一年后,实际月销售量P(台)与月次x之间存在如图所示函数关系(4月到12月近似符合二次函数关系).