题目内容
20.(1)已知f(x)=$\sqrt{\frac{1-x}{1+x}}$,α∈($\frac{π}{2}$,π),求f(cosα)+f(-cosα);(2)求值:sin50°(1+$\sqrt{3}$tan10°).
分析 (1)根据所给的函数式,代入自变量进行整理,观察分子和分母的特点,分子和分母同乘以一个代数式,使得分子和分母都变化成完全平方形式,开方合并同类型得到结果.
(2)先把原式中切转化成弦,利用两角和公式和整理后,运用诱导公式和二倍角公式化简整理求得答案.
解答 解:(1)∵f(x)=$\sqrt{\frac{1-x}{1+x}}$,α∈($\frac{π}{2}$,π),
∴f(cosα)+f(-cosα)=$\sqrt{\frac{1-cosα}{1+cosα}}$+$\sqrt{\frac{1+cosα}{1-cosα}}$=$\sqrt{\frac{(1-cosα)^{2}}{si{n}^{2}α}}$+$\sqrt{\frac{(1+cosα)^{2}}{si{n}^{2}α}}$=$\frac{|1-cosα|}{|sinα|}$+$\frac{|1+cosα|}{|sinα|}$=$\frac{2}{sinα}$;
(2)原式=sin50°•$\frac{cos10°+\sqrt{3}sin10°}{cos10°}$=cos40°•$\frac{2sin40°}{cos10°}$=$\frac{sin80°}{cos10°}$=$\frac{cos10°}{cos10°}$=1.
点评 本题主要考查了三角函数的恒等变换及其化简求值,以及两角和公式,诱导公式和二倍角公式的化简求值.考查了学生对三角函数基础知识的综合运用.

练习册系列答案
相关题目
10.设x>0,则$y=x+\frac{4}{x^2}$的最小值为( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | 3 | D. | $3\sqrt{2}$ |
11.已知集合A={x|y=log3(x-3)},B={x|x-3≤2},则A∪B=( )
| A. | R | B. | {x|x≥5} | C. | {x|x<3} | D. | {x|3<x≤5} |
8.若$\overrightarrow{OA}$=$\overrightarrow a$,$\overrightarrow{OB}$=$\overrightarrow b$,$\overrightarrow a$与$\overrightarrow b$不共线,则∠AOB平分线上的向量$\overrightarrow{OM}$为( )
| A. | $\frac{\overrightarrow a}{{|{\overrightarrow a}|}}+\frac{\overrightarrow b}{{|{\overrightarrow b}|}}$ | B. | $\frac{\overrightarrow a+\overrightarrow b}{{|{\overrightarrow a+\overrightarrow b}|}}$ | ||
| C. | $\frac{{|{\overrightarrow b}|\overrightarrow a-|{\overrightarrow a}|\overrightarrow b}}{{|{\overrightarrow a}|+|{\overrightarrow b}|}}$ | D. | $λ(\frac{\overrightarrow a}{{|{\overrightarrow a}|}}+\frac{\overrightarrow b}{{|{\overrightarrow b}|}})$,λ由$\overrightarrow{OM}$确定 |
5.已知函数f(x)=2x+$\frac{1}{{2}^{x+2}}$,则f(x)取最小值时对应的x的值为( )
| A. | -1 | B. | -$\frac{1}{2}$ | C. | 0 | D. | 1 |
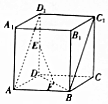 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1,BD的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1,BD的中点.