题目内容
12.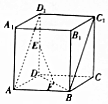 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1,BD的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1,BD的中点.(1)求证:EF∥平面ABC1D1;
(2)AA1=2$\sqrt{2}$,求异面直线EF与BC所成的角的大小.
分析 (1)连结BD1,推导出EF∥D1B,由此能证明EF∥平面ABC1D1.
(2)由EF∥BD1,知∠D1BC是异面直线EF与BC所成的角(或所成角的补角),由此能求出异面直线EF与BC所成的角的大小.
解答 证明:(1)连结BD1,
在△DD1B中,E、F分别是D1D、DB的中点,
∴EF是△DD1B的中位线,
∴EF∥D1B,
∵D1B?平面ABC1D1,EF?平面ABC1D1,
∴EF∥平面ABC1D1.
解:(2)∵AA1=2$\sqrt{2}$,AB=2,EF∥BD1,
∴∠D1BC是异面直线EF与BC所成的角(或所成角的补角),
在直四棱柱ABCD-A1B1C1D1中,BC⊥平面CDD1C1,CD1?平面CDD1C1,
∴BC⊥CD1.
在Rt△D1C1C中,BC=2,CD1=2$\sqrt{3}$,D1C⊥BC,
∴tan∠D1BC=$\frac{{D}_{1}C}{BC}=\sqrt{3}$,
∴∠D1BC=60°,
∴异面直线EF与BC所成的角的大小为60°.
点评 本题考查线面平行的证明,考查异面直线所成角的求法,考查空间中线线、线面、面面的位置关系等基础知识,考查推理论证能力、运算求解能力,考查数形结合合思想、化归与转化思想、函数与方程思想,是基础题.

练习册系列答案
相关题目
3.如果散点图中所有的样本点都落在一条斜率为2的直线上,则R2等于( )
| A. | 1 | B. | 2 | C. | 0 | D. | 不能确定 |
7.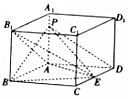 如图,在长方体ABCD-A1B1C1D1中,E是CD上一点,AB=AD=3,AA1=2,CE=1,P是AA1上一点,且DP∥平面AEB1,F是棱DD1与平面BEP的交点,则DF的长为( )
如图,在长方体ABCD-A1B1C1D1中,E是CD上一点,AB=AD=3,AA1=2,CE=1,P是AA1上一点,且DP∥平面AEB1,F是棱DD1与平面BEP的交点,则DF的长为( )
 如图,在长方体ABCD-A1B1C1D1中,E是CD上一点,AB=AD=3,AA1=2,CE=1,P是AA1上一点,且DP∥平面AEB1,F是棱DD1与平面BEP的交点,则DF的长为( )
如图,在长方体ABCD-A1B1C1D1中,E是CD上一点,AB=AD=3,AA1=2,CE=1,P是AA1上一点,且DP∥平面AEB1,F是棱DD1与平面BEP的交点,则DF的长为( )| A. | 1 | B. | $\frac{8}{9}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
4.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为4π,且其图象向右平移$\frac{π}{5}$个单位后得到函数g(x)=sinωx的图象,则φ等于( )
| A. | -$\frac{π}{10}$ | B. | -$\frac{π}{5}$ | C. | $\frac{π}{10}$ | D. | $\frac{π}{5}$ |
2.下列说法正确的是( )
| A. | “a>b”是“a2>b2”的充分不必要条件 | |
| B. | 命题“?x0∈R,$x_0^2+1<0$”的否定是“?x∈R,x2+1>0” | |
| C. | 关于x的方程x2+(a+1)x+a-2=0的两实根异号的充要条件是a<1 | |
| D. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为真命题 |
3.y=5-sin2x-4cosx最小值为( )
| A. | -2 | B. | 0 | C. | 1 | D. | -1 |