题目内容
11.幂函数f(x)=xa的图象经过点($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$),则1+logaf(4)=0.分析 根据幂函数f(x)的图象经过点($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$),求出幂函数的解析式,
再计算1+logaf(4)的值.
解答 解:幂函数f(x)=xa的图象经过点($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$),
∴${(\frac{1}{2})}^{α}$=$\frac{\sqrt{2}}{2}$,解得α=$\frac{1}{2}$,
∴f(x)=${x}^{\frac{1}{2}}$=$\sqrt{x}$;
∴f(4)=$\sqrt{4}$=2,
∴1+logaf(4)=1+${log}_{\frac{1}{2}}$2=1-1=0.
故答案为:0.
点评 本题考查了幂函数的图象与性质的应用问题,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.下列说法正确的是( )
| A. | “a>b”是“a2>b2”的充分不必要条件 | |
| B. | 命题“?x0∈R,$x_0^2+1<0$”的否定是“?x∈R,x2+1>0” | |
| C. | 关于x的方程x2+(a+1)x+a-2=0的两实根异号的充要条件是a<1 | |
| D. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为真命题 |
19.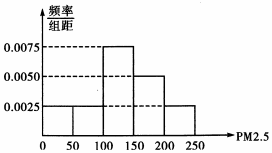 PM2.5是衡量空气污染程度的一个指标,为了了解某市空气质量情况,从去年每天的PM2.5值的数据中随机抽取40天的数据,其频率分布直方图如图所示.现将PM2.5的值划分为如下等级
PM2.5是衡量空气污染程度的一个指标,为了了解某市空气质量情况,从去年每天的PM2.5值的数据中随机抽取40天的数据,其频率分布直方图如图所示.现将PM2.5的值划分为如下等级
用频率估计概率.
(1)估计该市在下一年的360天中空气质量为一级天气的天数;
(2)在样本中,按照分层抽样的方法抽取8天的PM2.5值的数据,再从这8个数据中随机抽取5个,求一级、二级、三级、四级天气都有的概率;
(3)如果该市对环境进行治理,治理后经统计,每天PM2.5值X近似满足X~N(115,752),则治理后的PM2.5值的均值比治理前大约下降了多少?
 PM2.5是衡量空气污染程度的一个指标,为了了解某市空气质量情况,从去年每天的PM2.5值的数据中随机抽取40天的数据,其频率分布直方图如图所示.现将PM2.5的值划分为如下等级
PM2.5是衡量空气污染程度的一个指标,为了了解某市空气质量情况,从去年每天的PM2.5值的数据中随机抽取40天的数据,其频率分布直方图如图所示.现将PM2.5的值划分为如下等级| PM2.5 | [0,100) | [100,150) | [150,200) | [200,250] |
| 等级 | 一级 | 二级 | 三级 | 四级 |
(1)估计该市在下一年的360天中空气质量为一级天气的天数;
(2)在样本中,按照分层抽样的方法抽取8天的PM2.5值的数据,再从这8个数据中随机抽取5个,求一级、二级、三级、四级天气都有的概率;
(3)如果该市对环境进行治理,治理后经统计,每天PM2.5值X近似满足X~N(115,752),则治理后的PM2.5值的均值比治理前大约下降了多少?
6.将石子摆成如图的梯形形状,称数列5,9,14,20,…为“梯形数”.根据图形的构成,此数列的第2 016项与5的差,即a2016-5=( )


| A. | 2 018×2 014 | B. | 2 018×2 013 | C. | 1 011×2 015 | D. | 1 010×2 012 |
16.函数f(x)=|sinx+2cosx|+|2sinx-cosx|的最小正周期为( )
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
3.y=5-sin2x-4cosx最小值为( )
| A. | -2 | B. | 0 | C. | 1 | D. | -1 |
20.已知f(x)=2xf′(1)+lnx,则f′(1)=( )
| A. | -e | B. | -1 | C. | 1 | D. | e |