已知函数f(x)=2x+$\frac{1}{{2}^{x+2}}$.则f(x)取最小值时对应的x的值为( )A．-1B．-$\frac{1}{2}$C．0D．1 题目和参考答案——青夏教育精英家教网—

题目内容

5．已知函数f（x）=2^x+$\frac{1}{{2}^{x+2}}$，则f（x）取最小值时对应的x的值为（　　）

A．

-1

B．

-$\frac{1}{2}$

C．

D．

分析根据基本不等式的性质求出x的值即可．

解答解：2^x＞0，∴2^x+$\frac{1}{{2}^{x+2}}$≥2$\sqrt{{2}^{x}•\frac{1}{{2}^{x+2}}}$=1，
当且仅当2^x=$\frac{1}{{2}^{x+2}}$，即x=-1时“=”成立，
故选：A．

点评本题考查了求函数的最值问题，考查基本不等式的性质，是一道基础题．

练习册系列答案

{k|k≥$\frac{3}{4}$或k≤-4}

B．

{k|-4≤k≤$\frac{3}{4}$}

C．

{k|-$\frac{3}{4}$≤k＜4}

D．

以上都不对

16．已知i是虚数单位，且复数z满足$z=\frac{2+ai}{2+i}（{a∈R}）$，若z为实数，则实数a的值为（　　）

13．已知函数h（x）=x²+2x+alnx（a∈R），f（x）=（x²-2x）lnx+ax²+2．
（1）讨论函数y=h（x）的单调性；
（2）当a＞0时，设函数g（x）=f（x）-x-2且函数g（x）有且只有一个零点，若e^-2＜x＜e，g（x）≤m，求m的取值范围．

20．（1）已知f（x）=$\sqrt{\frac{1-x}{1+x}}$，α∈（$\frac{π}{2}$，π），求f（cosα）+f（-cosα）；
（2）求值：sin50°（1+$\sqrt{3}$tan10°）．

10．

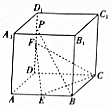如图，在棱长为4的正方体ABCD-A₁B₁C₁D₁中，E、F分别是AB、DD₁的中点，点P是DD₁上一点，且PB∥平面CEF，则四棱锥P-ABCD外接球的体积为$\frac{41\sqrt{41}}{6}π$．

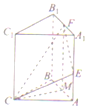17．已知数列{a_n}的前n项和为S_n=2a_n-1，则满足$\frac{{a}_{n}}{n}≤2$的最大正整数n的值为（　　）

14．

在三棱柱ABC-A₁B₁C₁中，已知侧按AA₁⊥底面ABC，且四边形AA₁B₁B是边长为2的正方形，CA=CB，点M为棱AB的中点，点E，F分别在按AA₁，A₁B₁上
（Ⅰ）若点F为棱A₁B₁的中点，证明：平面ABC₁⊥平面CMF
（Ⅱ）若AE=$\frac{1}{2}$，A₁F=$\frac{3}{4}$，且CA⊥CB，求直线AC₁与平面CEF所成角的正弦值．

16．函数f（x）=|sinx+2cosx|+|2sinx-cosx|的最小正周期为（　　）

试题分类