题目内容
4.已知圆x2+y2=4,直线l:y=x+b,若圆x2+y2=4上恰有4个点到直线l的距离都等于1,则b的取值范围为( )| A. | (-1,1) | B. | [-1,1] | C. | $[{-\sqrt{2},\sqrt{2}}]$ | D. | $({-\sqrt{2},\sqrt{2}})$ |
分析 若圆C上恰有4个点到直线l的距离等于1,则O到直线l:y=x+b的距离d小于1,代入点到直线的距离公式,可得答案.
解答 解:由圆C的方程:x2+y2=4,可得圆C的圆心为原点O(0,0),半径为2
若圆C上恰有4个点到直线l的距离等于1,则O到直线l:y=x+b的距离d小于1,
直线l的一般方程为:x-y+b=0,∴d=$\frac{|b|}{\sqrt{2}}$<1
解得-$\sqrt{2}<b<\sqrt{2}$,即b的取值范围为(-$\sqrt{2},\sqrt{2}$).
故选:D.
点评 本题考查实数的取值范围的求法,考查圆、直线方程、点到直线距离公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
相关题目
15.角A、B、C为△ABC的三个内角,函数f(x)=2sin(x-A)cosx+sin(B+C)(x∈R)的图象关于直线x=$\frac{5π}{12}$对称,则A=( )
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |
19.在平行四边形ABCD中,AB=2,∠DAB=$\frac{2}{3}$π,E是BC的中点,$\overrightarrow{AE}•\overrightarrow{BD}$=2,则AD=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.若直线x-y+m=0被圆(x-1)2+y2=5截得的弦长为2$\sqrt{3}$,则m的值为( )
| A. | 1 | B. | -3 | C. | 1或-3 | D. | 2 |
13.已知z=$\frac{3i}{1-i}$,则复数$\overline z$在复平面对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
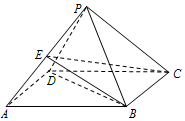 已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,PA=$\sqrt{6}$.
已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,PA=$\sqrt{6}$.