题目内容
16．${（{2x-\frac{1}{{\sqrt{x}}}}）^5}$的展开式中，$\sqrt{x}$的系数为-40．分析 在二项展开式的通项公式中，令x的幂指数等于$\frac{1}{2}$，求出r的值，即可求得开式中x的系数．
解答 解：${（{2x-\frac{1}{{\sqrt{x}}}}）^5}$的展开式的通项为C5r25-r（-1）rx${\;}^{5-\frac{3r}{2}}$，
令5-$\frac{3}{2}$r=$\frac{1}{2}$，求得 r=3，
∴$\sqrt{x}$的系数为C5325-3（-1）3=-40
故答案为：-40．
点评 本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
6．已知函数f（x）=sin（2x+φ），将其图象向左平移$\frac{π}{6}$个单位长度后得到的函数为偶函数，则φ的最小正值为（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{3}$ | D． | $\frac{2π}{3}$ |
4．已知圆x2+y2=4，直线l：y=x+b，若圆x2+y2=4上恰有4个点到直线l的距离都等于1，则b的取值范围为（ ）
| A． | （-1，1） | B． | [-1，1] | C． | $[{-\sqrt{2}，\sqrt{2}}]$ | D． | $（{-\sqrt{2}，\sqrt{2}}）$ |
8．函数$f（x）=cos（{ωx+\frac{π}{6}}）$（ω＞0）的最小正周期为π，则f（x）满足（ ）
| A． | 在$（{0，\frac{π}{3}}）$上单调递增 | B． | 图象关于直线$x=\frac{π}{6}$对称 | ||
| C． | $f（{\frac{π}{3}}）=\frac{{\sqrt{3}}}{2}$ | D． | 当$x=\frac{5π}{12}$时有最小值-1 |
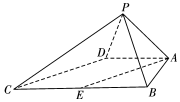如图，四棱锥P-ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB与△PAD都是边长为2的等边三角形，E是BC的中点．
，
，若
，则实数的a值是____________．