题目内容
9.若直线x-y+m=0被圆(x-1)2+y2=5截得的弦长为2$\sqrt{3}$,则m的值为( )| A. | 1 | B. | -3 | C. | 1或-3 | D. | 2 |
分析 先求出圆(x-1)2+y2=5的圆心C(1,0),半径r=$\sqrt{5}$,再求出圆心C(1,0)到直线x-y+m=0的距离d,由此利用直线x-y+m=0被圆(x-1)2+y2=5截得的弦长为2$\sqrt{3}$,根据勾股定理能求出m.
解答 解:圆(x-1)2+y2=5的圆心C(1,0),半径r=$\sqrt{5}$,
圆心C(1,0)到直线x-y+m=0的距离:d=$\frac{|1-0+m|}{\sqrt{2}}$=$\frac{|1+m|}{\sqrt{2}}$,
∵直线x-y+m=0被圆(x-1)2+y2=5截得的弦长为2$\sqrt{3}$,
∴$\sqrt{5-(\frac{|1+m|}{\sqrt{2}})^{2}}$=($\frac{2\sqrt{3}}{2}$)2,
解得m=1或m=-3.
故选:C.
点评 本题考查直线被圆截得的弦长的求法及应用,考查圆、直线方程、点到直线距离公式等基础知识,考查推理论证能力、运算求解能力、化归与转化思想,是中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
20.椭圆$\frac{{x}^{2}}{a}$+y2=1(a>1)与双曲线$\frac{{y}^{2}}{b}$-y2=1(b>0)有相同的焦点F1、F2,若P为两曲线的一个交点,则△PF1F2的面积为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
4.已知圆x2+y2=4,直线l:y=x+b,若圆x2+y2=4上恰有4个点到直线l的距离都等于1,则b的取值范围为( )
| A. | (-1,1) | B. | [-1,1] | C. | $[{-\sqrt{2},\sqrt{2}}]$ | D. | $({-\sqrt{2},\sqrt{2}})$ |
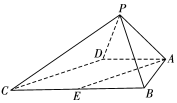 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点. 在R上是单调增函数,求实数a的取值范围。
在R上是单调增函数,求实数a的取值范围。