题目内容
15.角A、B、C为△ABC的三个内角,函数f(x)=2sin(x-A)cosx+sin(B+C)(x∈R)的图象关于直线x=$\frac{5π}{12}$对称,则A=( )| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |
分析 根据三角形内角和定理和诱导公式化简,结合三角函数的性质,可知x=$\frac{5π}{12}$时,f(x)取得最值.可得A的值.
解答 解:由函数f(x)=2sin(x-A)cosx+sin(B+C)
=2sinxcosxcosA-2cos2xsinA+sinA=sin2xcosA-sinA(cos2x+1)+sinA=sin2xcosA-cos2xsinA
∵函数f(x)关于直线x=$\frac{5π}{12}$对称,
当x=$\frac{5π}{12}$时,f(x)=sin$\frac{5π}{6}$cosA-cos$\frac{5π}{6}$sinA=$\frac{1}{2}$cosA+$\frac{\sqrt{3}}{2}$sinA=sin(A+$\frac{π}{6}$)
若x=$\frac{5π}{12}$时,f(x)取得最小值,即$\frac{π}{6}+A=kπ-\frac{π}{2}$,k∈Z.
∵0<A<π
∴A=$\frac{π}{3}$.
若x=$\frac{5π}{12}$时,f(x)取得最大值,即$\frac{π}{6}+A=kπ+\frac{π}{2}$,k∈Z.
∵0<A<π
∴A=$\frac{π}{3}$.
综上可得A=$\frac{π}{3}$.
故选D
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
5.设向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(m+1,-m),$\overrightarrow{a}$⊥$\overrightarrow{b}$,则实数m的值为( )
| A. | -1 | B. | 1 | C. | -$\frac{1}{3}$ | D. | $-\frac{2}{3}$ |
6.已知函数f(x)=sin(2x+φ),将其图象向左平移$\frac{π}{6}$个单位长度后得到的函数为偶函数,则φ的最小正值为( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
3.sin210°的值等于( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
10.若点P(sinθ,cosθ)在直线2x+y=0上,则tan2θ=( )
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{3}$ | C. | -$\frac{4}{3}$ | D. | $\frac{4}{5}$ |
20.椭圆$\frac{{x}^{2}}{a}$+y2=1(a>1)与双曲线$\frac{{y}^{2}}{b}$-y2=1(b>0)有相同的焦点F1、F2,若P为两曲线的一个交点,则△PF1F2的面积为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
4.已知圆x2+y2=4,直线l:y=x+b,若圆x2+y2=4上恰有4个点到直线l的距离都等于1,则b的取值范围为( )
| A. | (-1,1) | B. | [-1,1] | C. | $[{-\sqrt{2},\sqrt{2}}]$ | D. | $({-\sqrt{2},\sqrt{2}})$ |
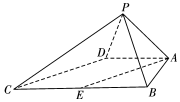 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.