题目内容
14.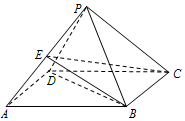 已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,PA=$\sqrt{6}$.
已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,PA=$\sqrt{6}$.(Ⅰ)求证:BD⊥PC;
(Ⅱ)若E是PA的中点,求三棱锥P-BCE的体积.
分析 (I)连接AC交BD于O点,由BD⊥AC,BD⊥OP得出BD⊥平面PAC,故PC⊥BD;
(II)利用勾股定理计算OA,OP,证明OA⊥OP,得出三角形PCE的面积,于是VP-BCE=VB-PCE=$\frac{1}{3}$S△PCE•OP.
解答 证明:(I)连接AC交BD于O点,
∵四边形ABCD是菱形,∴AC⊥BD,O是BD的中点,
∵PB=PD,∴PO⊥BD,
又AC∩OP=O,AC?平面PAC,OP?平面PAC,
∴BD⊥平面PAC,又PC?平面PAC,
∴BD⊥PC.
(II)∵四边形ABCD是菱形,∠BAD=60°,
∴BD=AB=AD=2,∴OB=1,OA=$\sqrt{3}$,
∴OP=$\sqrt{P{B}^{2}-O{B}^{2}}$=$\sqrt{3}$,∴OA2+OP2=PA2,即OA⊥OP.
∴S△PCE=$\frac{1}{2}$S△PAC=S△POA=$\frac{1}{2}$×$\sqrt{3}×\sqrt{3}$=$\frac{3}{2}$.
∴又OB⊥平面PAC,
∴VP-BCE=VB-PCE=$\frac{1}{3}$S△PCE•OB=$\frac{1}{3}×$$\frac{3}{2}$×1=$\frac{1}{2}$.
点评 题考查了线面垂直的判定与性质,棱锥的体积计算,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.设向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(m+1,-m),$\overrightarrow{a}$⊥$\overrightarrow{b}$,则实数m的值为( )
| A. | -1 | B. | 1 | C. | -$\frac{1}{3}$ | D. | $-\frac{2}{3}$ |
6.已知函数f(x)=sin(2x+φ),将其图象向左平移$\frac{π}{6}$个单位长度后得到的函数为偶函数,则φ的最小正值为( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
3.sin210°的值等于( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
4.已知圆x2+y2=4,直线l:y=x+b,若圆x2+y2=4上恰有4个点到直线l的距离都等于1,则b的取值范围为( )
| A. | (-1,1) | B. | [-1,1] | C. | $[{-\sqrt{2},\sqrt{2}}]$ | D. | $({-\sqrt{2},\sqrt{2}})$ |