题目内容
己知⊙O:x2+y2=6,P为⊙O上动点,过P作PM⊥x轴于M,N为PM上一点,且
=
.
(Ⅰ)求点N的轨迹C的方程;
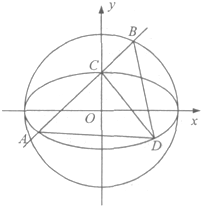
(Ⅱ)若A(2,1),B(3,0),过B的直线与曲线C相交于D、E两点,则kAD+kAE是否为定值?若是,求出该值;若不是,说明理由.
| PM |
| 2 |
| NM |
(Ⅰ)求点N的轨迹C的方程;
(Ⅱ)若A(2,1),B(3,0),过B的直线与曲线C相交于D、E两点,则kAD+kAE是否为定值?若是,求出该值;若不是,说明理由.
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)设M(x,y),则可设P(x,y0),Q(x,0),根据又
=
,可确定y0=3y,进而可知点P的坐标代入圆的方程,求得曲线C的方程.
(Ⅱ)设D(x1,y1),E(x2,y2),设出过点B的直线DE的方程,与题意方程联立,利用韦达定理求出横坐标的和与乘积,求出kAD+kAE化简即可判断否为定值.
| PM |
| 2 |
| NM |
(Ⅱ)设D(x1,y1),E(x2,y2),设出过点B的直线DE的方程,与题意方程联立,利用韦达定理求出横坐标的和与乘积,求出kAD+kAE化简即可判断否为定值.
解答:
解:(Ⅰ)设N(x,y),P(x0,y0),则M(x0,0),
=(0,-y0),
=(x0-x,-y)
由
=
,得
,
∴
…(3分)
由于点P在圆O:x2+y2=6上,则有x2+(
y)2=6,即
+
=1.
∴点N的轨迹C的方程为
+
=1.…(6分)
(Ⅱ) 设D(x1,y1),E(x2,y2),过点B的直线DE的方程为y=k(x-3),
由
消去y得:(2k2+1)x2-12k2x+18k2-6=0,其中△>0
∴x1+x2=
,x1x2=
;…(8分)
∴kAD+kAE=
+
=
+
=
…(10分)
=
=
=-2
∴kAD+kAE是定值-2.…(13分)
| PM |
| NM |
由
| PM |
| 2 |
| NM |
|
∴
|
由于点P在圆O:x2+y2=6上,则有x2+(
| 2 |
| x2 |
| 6 |
| y2 |
| 3 |
∴点N的轨迹C的方程为
| x2 |
| 6 |
| y2 |
| 3 |
(Ⅱ) 设D(x1,y1),E(x2,y2),过点B的直线DE的方程为y=k(x-3),
由
|
∴x1+x2=
| 12k2 |
| 2k2+1 |
| 18k2-6 |
| 2k2+1 |
∴kAD+kAE=
| y1-1 |
| x1-2 |
| y2-1 |
| x2-2 |
| kx1-(3k+1) |
| x1-2 |
| kx2-(3k+1) |
| x2-2 |
=
| 2kx1x2-(5k+1)(x1+x2)+12k+4 |
| x1x2-2(x1+x2)+4 |
=
2k•
| ||||
|
| -4k2+4 |
| 2k2-2 |
∴kAD+kAE是定值-2.…(13分)
点评:本题主要考查了椭圆的应用,韦达定理等知识都有涉及,直线的斜率,综合性很强.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
已知函数f(x)是奇函数,且x∈(0,2)时,f(x)=2x,则f(-1)=( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
下列命题中的假命题是( )
| A、?x∈R,lgx=0 | ||
| B、?x∈R,tanx=1 | ||
| C、?x∈R,2x>0 | ||
D、?x∈R,sinx+cosx=
|
 若中心在原点的椭圆C1:
若中心在原点的椭圆C1: