题目内容
已知函数f(x)是奇函数,且x∈(0,2)时,f(x)=2x,则f(-1)=( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
考点:函数的值
专题:函数的性质及应用
分析:由题意可得f(-1)=-f(1),计算求得结果.
解答:
解:∵函数f(x)是奇函数,且x∈(0,2)时,f(x)=2x,
则f(-1)=-f(1)=-21=-2,
故选:B.
则f(-1)=-f(1)=-21=-2,
故选:B.
点评:本题主要考查利用函数的奇偶性求函数的值,属于基础题.

练习册系列答案
相关题目
对于函数f(x)=cos2(x-
)+sin2(x+
)-1,下列选项中正确的是( )
| π |
| 12 |
| π |
| 12 |
A、f(x)在(
| ||||
| B、f(x)的图象关于原点对称 | ||||
| C、f(x)的最小正周期为2π | ||||
| D、f(x)的最大值为1 |
已知存在正数a,b,c满足
≤
≤2,clnb=a+clnc,则ln
的取值范围是( )
| 1 |
| e |
| c |
| a |
| b |
| a |
A、[1,
| ||
| B、[1,+∞) | ||
| C、(-∞,e-1] | ||
| D、[1,e-1] |
对于空间的两条直线m、n和一个平面α,下列命题中的真命题是( )
| A、若m∥α,n∥α,则m∥n |
| B、若m∥α,n?α,则m∥n |
| C、若m∥α,n⊥α,则m∥n |
| D、若m⊥α,n⊥α,则m∥n |
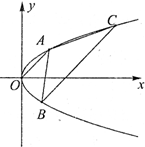 已知点A,B,C是抛物线L:y2=2px(p>0)上的不同的三点,O为坐标原点,直线OA∥BC,且抛物线L的准线方程为x=-1.
已知点A,B,C是抛物线L:y2=2px(p>0)上的不同的三点,O为坐标原点,直线OA∥BC,且抛物线L的准线方程为x=-1.