题目内容
已知抛物线C:y2=12x,点M(a,0),过M的直线l交抛物线C于A,B两点.
(Ⅰ)若a=1,抛物线C的焦点与AB中点的连线垂直于x轴,求直线l的方程;
(Ⅱ)设a为小于零的常数,点A关于x轴的对称点为A′,求证:直线A′B过定点.
(Ⅰ)若a=1,抛物线C的焦点与AB中点的连线垂直于x轴,求直线l的方程;
(Ⅱ)设a为小于零的常数,点A关于x轴的对称点为A′,求证:直线A′B过定点.
考点:直线与圆锥曲线的关系,恒过定点的直线,与直线关于点、直线对称的直线方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)设过点M(1,0)的直线l的方程为y=k(x-1),代入抛物线方程,消去y,利用F与AB中点的连线垂直于x轴,结合韦达定理,求出k,即可求直线l的方程;
(Ⅱ)因为点A关于x轴的对称点为A′,所以A′(x1,-y1),直线A′B:y-y2=
(x-x2),利用韦达定理,结合抛物线方程,即可证明结论.
(Ⅱ)因为点A关于x轴的对称点为A′,所以A′(x1,-y1),直线A′B:y-y2=
| y2+y1 |
| x2-x1 |
解答:
(Ⅰ)解:由已知,抛物线C:y2=12x,的焦点坐标为F(3,0).…(1分)
设过点M(1,0)的直线l的方程为y=k(x-1),
代入抛物线方程,消去y可得k2x2-(2k2+12)x+k2=0.…(2分)
设A(x1,y1),B(x2,y2),则x1+x2=
.…(3分)
因为F与AB中点的连线垂直于x轴,所以
=3,即
=3.…(4分)
解得k=±
,.…(5分)
所以,直线l的方程为y=±
(x-1).…(6分)
(Ⅱ)证明:设直线l的方程为y=(x-a).
代入抛物线方程,消去y可得k2x2-(2ak2+12)x+a2k2=0,…(7分)
则k2≠0,且△=48ak2+144>0,即k≠0,且ak2+3>0.
x1+x2=
,x1x2=a2.…(8分)
因为点A关于x轴的对称点为A′,所以A′(x1,-y1),直线A′B:y-y2=
(x-x2),
又y12=12x1,y22=12x2,所以y=
(x-x2)+y2,…(10分)
所以y=
x-
.…(11分)
因为y12y22=144x1x2=144a2,又y1,y2同号,a<0,
所以y1y2=-12a,…(12分)
所以直线直线A′B的方程为y=
(x+a),…(13分)
所以,直线直线A′B恒过定点(-a,0).…(14分)
设过点M(1,0)的直线l的方程为y=k(x-1),
代入抛物线方程,消去y可得k2x2-(2k2+12)x+k2=0.…(2分)
设A(x1,y1),B(x2,y2),则x1+x2=
| 2k2+12 |
| k2 |
因为F与AB中点的连线垂直于x轴,所以
| x1+x2 |
| 2 |
| k2+6 |
| k2 |
解得k=±
| 3 |
所以,直线l的方程为y=±
| 3 |
(Ⅱ)证明:设直线l的方程为y=(x-a).
代入抛物线方程,消去y可得k2x2-(2ak2+12)x+a2k2=0,…(7分)
则k2≠0,且△=48ak2+144>0,即k≠0,且ak2+3>0.
x1+x2=
| 2ak2+12 |
| k2 |
因为点A关于x轴的对称点为A′,所以A′(x1,-y1),直线A′B:y-y2=
| y2+y1 |
| x2-x1 |
又y12=12x1,y22=12x2,所以y=
| 12 |
| y2-y1 |
所以y=
| 12 |
| y2-y1 |
| y1y2 |
| y2-y1 |
因为y12y22=144x1x2=144a2,又y1,y2同号,a<0,
所以y1y2=-12a,…(12分)
所以直线直线A′B的方程为y=
| 12 |
| y2-y1 |
所以,直线直线A′B恒过定点(-a,0).…(14分)
点评:本题考查直线与抛物线的位置关系,考查直线方程的求解,考查学生的计算能力,属于中档题.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
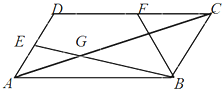 如图所示,在平行四边形ABCD中,∠BAD=
如图所示,在平行四边形ABCD中,∠BAD= 如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=
如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=