题目内容
已知函数f（x）=sin（ωx+φ） (ω＞0，0＜φ＜
)的最小正周期为π，
（1）求当f（x）为偶函数时φ的值；
（2）若f（x）的图象过点（
，
），求f（x）的单调递增区间．
| 2π |
| 3 |
（1）求当f（x）为偶函数时φ的值；
（2）若f（x）的图象过点（
| π |
| 6 |
| ||
| 2 |
考点：函数y=Asin（ωx+φ）的图象变换,三角函数的周期性及其求法
专题：计算题,三角函数的图像与性质
分析：（1）依题意知T=π，ω=2，当f（x）=sin（2x+φ）为偶函数时，φ=kπ+
（k∈Z），又0＜φ＜
，于是可求得φ的值；
（2）由f（
）=sin（
+φ）=
及0＜φ＜
可求得φ=
，从而可求得f（x）的单调递增区间．
| π |
| 2 |
| 2π |
| 3 |
（2）由f（
| π |
| 6 |
| π |
| 3 |
| ||
| 2 |
| 2π |
| 3 |
| π |
| 3 |
解答：
解：（1）∵T=π，
∴ω=
=2，
∴f（x）=sin（2x+φ），
∴当f（x）=sin（2x+φ）为偶函数时，
φ=kπ+
（k∈Z），又0＜φ＜
，
∴φ=
；
（2）∵f（
）=sin（
+φ）=
，
又0＜φ＜
，
∴
＜φ+
＜π，
∴φ+
=
，
解得φ=
，
∴f（x）=sin（2x+
）；
由2kπ-
≤2x+
≤2kπ+
（k∈Z）得：kπ-
≤x≤kπ+
（k∈Z）．
∴f（x）的单调递增区间为[kπ-
，kπ+
]（k∈Z）．
∴ω=
| 2π |
| T |
∴f（x）=sin（2x+φ），
∴当f（x）=sin（2x+φ）为偶函数时，
φ=kπ+
| π |
| 2 |
| 2π |
| 3 |
∴φ=
| π |
| 2 |
（2）∵f（
| π |
| 6 |
| π |
| 3 |
| ||
| 2 |
又0＜φ＜
| 2π |
| 3 |
∴
| π |
| 3 |
| π |
| 3 |
∴φ+
| π |
| 3 |
| 2π |
| 3 |
解得φ=
| π |
| 3 |
∴f（x）=sin（2x+
| π |
| 3 |
由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
∴f（x）的单调递增区间为[kπ-
| 5π |
| 12 |
| π |
| 12 |
点评：本题考查函数y=Asin（ωx+φ）的图象变换，考查正弦函数的单调性，（1）与（2）中求φ的值是难点，考查运算求解能力，属于中档题．
练习册系列答案
相关题目
椭圆有一个焦点固定，并通过两个已知点，且该焦点到这两个定点不等距．则该椭圆另一个焦点的轨迹类型是（ ）
| A、椭圆型 | B、双曲线型 |
| C、抛物线型 | D、非圆锥曲线型 |
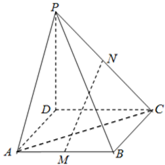如图，P是正方形ABCD所在平面外一点，且PD⊥AD，PD⊥DC，PD=3，AD=2，若M、N分别是AB、PC的中点．