题目内容
已知集合M={x|2x2-(2a+1)x+a>0,a>
},集合N={x|?t∈R,使得t2+t+1≤x成立},若x∈N是x∈M的充分不必要条件,求实数a的取值范围.
| 1 |
| 2 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:分别求出集合M,N成立的等价条件,利用充分不必要条件的定义即可得到结论.
解答:
解:∵2x2-(2a+1)x+a>0,
∴(x-a)(2x-1)>0,
∵a>
,
∴不等式的解为x>a或x<
,
即M={x|x>a或x<
}.
∵t2+t+1=(t+
)2+
≥
,
∴若?t∈R,使得t2+t+1≤x成立,
则x≥
,
即N={x|x≥
}.
若x∈N是x∈M的充分不必要条件,
则N?M,
即
<a<
,
∴实数a的取值范围是
<a<
.
∴(x-a)(2x-1)>0,
∵a>
| 1 |
| 2 |
∴不等式的解为x>a或x<
| 1 |
| 2 |
即M={x|x>a或x<
| 1 |
| 2 |
∵t2+t+1=(t+
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
∴若?t∈R,使得t2+t+1≤x成立,
则x≥
| 3 |
| 4 |
即N={x|x≥
| 3 |
| 4 |
若x∈N是x∈M的充分不必要条件,
则N?M,
即
| 1 |
| 2 |
| 3 |
| 4 |
∴实数a的取值范围是
| 1 |
| 2 |
| 3 |
| 4 |
点评:本题主要考查充分条件和必要条件的应用,利用不等式的性质求出M,N的等价条件是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2
如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2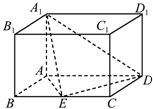 如图,长方体ABCD-A1B1C1D1中,E为线段BC的中点,AB=1,AD=2,AA1=
如图,长方体ABCD-A1B1C1D1中,E为线段BC的中点,AB=1,AD=2,AA1=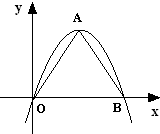 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.