题目内容
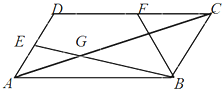如图所示，在平行四边形ABCD中，∠BAD=| π |
| 3 |
|
| ||
|
|
|
| ||
|
|
（1）若t=
| 1 |
| 2 |
| AB |
| AD |
| AG |
（2）求
| BG |
| BF |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：（1）由点E、G、B三点共线，得
=m
+(1-m)
=
m
+（1-m）
，又点G在AC上，则
=n
，即
=n(
+
)，由平面向量基本定理可得关于m、n的方程组，解出后可得结论；
（2）同（1）可用平面向量基本定理表示出
，进而可得
、
，从而可把
•
表示为t的函数，用导数可得该函数的最值，于是得到答案；
| AG |
| AE |
| AB |
| 1 |
| 2 |
| AD |
| AB |
| AG |
| AC |
| AG |
| AD |
| AB |
（2）同（1）可用平面向量基本定理表示出
| AG |
| BG |
| BF |
| BG |
| BF |
解答：
解：（1）若t=
，则
=
，
=
，
∵点E、G、B三点共线，
∴
=m
+(1-m)
=
m
+（1-m）
，
设
=n
，则
=n(
+
)，
∴
m
+（1-m）
=n(
+
)，则
，
解得m=
，n=
，
∴
=
(
+
)；
（2）
=m
+(1-m)
=m（1-t）
+（1-m）
，
设
=n
，则
=n(
+
)，
则
，得n=
，
∴
=
(
+
)，
则
=
-
=
（
+
）-
=
-
，
=
+
=
-t
，
而
•
=|
||
|cos∠BAD=2×1×cos
=1，
∴
•
=（
-
）•（
-t
）=
+
-
-
=
，
令y=
（0≤t≤1），
y'=
＞0，
∴y=
在t∈[0，1]上递增，
t=0时ymin=0，t=1时ymax=3，
∴
•
的取值范围为[0，3]．
| 1 |
| 2 |
| CF |
| 1 |
| 2 |
| CD |
| DE |
| 1 |
| 2 |
| DA |
∵点E、G、B三点共线，
∴
| AG |
| AE |
| AB |
| 1 |
| 2 |
| AD |
| AB |
设
| AG |
| AC |
| AG |
| AD |
| AB |
∴
| 1 |
| 2 |
| AD |
| AB |
| AD |
| AB |
|
解得m=
| 2 |
| 3 |
| 1 |
| 3 |
∴
| AG |
| 1 |
| 3 |
| AD |
| AB |
（2）
| AG |
| AE |
| AB |
| AD |
| AB |
设
| AG |
| AC |
| AG |
| AD |
| AB |
则
|
| 1-t |
| 2-t |
∴
| AG |
| 1-t |
| 2-t |
| AD |
| AB |
则
| BG |
| AG |
| AB |
| 1-t |
| 2-t |
| AD |
| AB |
| AB |
| 1-t |
| 2-t |
| AD |
| 1 |
| 2-t |
| AB |
| BF |
| BC |
| CF |
| AD |
| AB |
而
| AB |
| AD |
| AB |
| AD |
| π |
| 3 |
∴
| BG |
| BF |
| 1-t |
| 2-t |
| AD |
| 1 |
| 2-t |
| AB |
| AD |
| AB |
| 1-t |
| 2-t |
| 4t |
| 2-t |
| t(1-t) |
| 2-t |
| 1 |
| 2-t |
| t2+2t |
| 2-t |
令y=
| t2+2t |
| 2-t |
y'=
| -(t-2)2+8 |
| (2-t)2 |
∴y=
| t2+2t |
| 2-t |
t=0时ymin=0，t=1时ymax=3，
∴
| BG |
| BF |
点评：本题考查平面向量数量积的运算、平面向量基本定理、三点共线的条件等知识，考查函数思想，考查学生综合运用知识分析解决问题的能力．
练习册系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜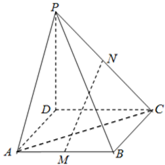
如图，P是正方形ABCD所在平面外一点，且PD⊥AD，PD⊥DC，PD=3，AD=2，若M、N分别是AB、PC的中点．
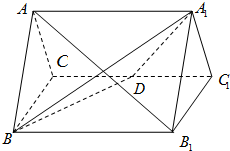如图，正三棱柱ABC-A1B1C1的所有棱长都为2，D为CC1的中点．
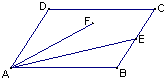如图，平行四边形ABCD中，AB=3，BC=2，