题目内容
将凸n边形A1A2…An的边与对角线染上红、蓝两色之一，使得没有三边均为蓝色的三角形．对k=1，2，…，n，记bk由顶点Ak出的蓝色边的条数，求证：b1+b2+…bn≤
．
| n2 |
| 2 |
考点：进行简单的合情推理
专题：综合题,推理和证明
分析：不妨设b=max{b1，b2，…，bn}，并且由点A向A1，A2，…，Ab，引出b条蓝色边，则A1，A2，…，Ab之间无蓝色边，A1，A2，…，Ab以外的n-b个点，每点至多引出b条蓝色边，可得蓝色边总数，利用基本不等式，即可得证．
解答：
证明：不妨设b=max{b1，b2，…，bn}，
并且由点A向A1，A2，…，Ab，引出b条蓝色边，则A1，A2，…，Ab之间无蓝色边，A1，A2，…，Ab以外的n-b个点，每点至多引出b条蓝色边，
因此蓝色边总数≤（n-b）b≤[
]2=
，
故b1+b2+…bn≤2×
=
．命题得证．
并且由点A向A1，A2，…，Ab，引出b条蓝色边，则A1，A2，…，Ab之间无蓝色边，A1，A2，…，Ab以外的n-b个点，每点至多引出b条蓝色边，
因此蓝色边总数≤（n-b）b≤[
| (n-b)+b |
| 2 |
| n2 |
| 4 |
故b1+b2+…bn≤2×
| n2 |
| 4 |
| n2 |
| 2 |
点评：本题考查合情推理，考查学生分析解决问题的能力，考查基本不等式的运用，属于中档题．
练习册系列答案
全能测控一本好卷系列答案
相关题目
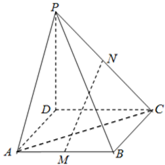如图，P是正方形ABCD所在平面外一点，且PD⊥AD，PD⊥DC，PD=3，AD=2，若M、N分别是AB、PC的中点．
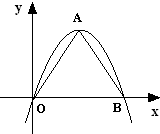如果一条抛物线y=ax2+bx+c（a≠0）与x轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”．
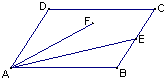如图，平行四边形ABCD中，AB=3，BC=2，