题目内容

求曲线C：x2+y2=
5
2
在A（1，
3
2
）处切线的斜率．
考点：圆的切线方程
专题：计算题,直线与圆
分析：求出CA的斜率，即可求出曲线C：x2+y2=
5
2
在A（1，
3
2
）处的切线斜率．
解答： 解：由于kCA=
3
2
，
可得曲线C：x2+y2=
5
2
在A（1，
3
2
）处的切线斜率为-
2
3
3
．
点评：本题考查圆的切线斜率，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
已知偶函数f（x）在[0，+∞）上为增函数，且f（2x-1）＜f（1），求x的取值范围．
已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的右顶点和右焦点分别为A（a，0）、F（c，0），若直线x=
a2
c
上存在点P使得∠APF=30°，则刻双曲线的离心率的取值范围是（　　）
A、（1，
3+
17
2
]
B、[
3+
17
2
，+∞）
C、（1，2]
D、[2，+∞）
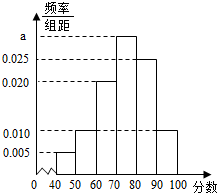从某校高三年级学生中抽取40名学生，将他们高中学业水平考试的数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：[40，50），[50，60），…，[90，100]后得到如图的频率分布直方图．
（1）若该校高三年级有640人，试估计这次学业水平考试的数学成绩不低于60分的人数及相应的平均分；
（2）若从[40，50）与[90，100]这两个分数段内的学生中随机选取两名学生，求这两名学生成绩之差的绝对值不大于10的概率．
已知集合A={x|1≤2x≤8}，B={x|-1≤log3x≤2}
（1）求A∪B，B∩（∁RA）．
（2）已知非空集合C={x|1＜x＜a}，C?B，求实数a的取值范围．
已知函数f（x）=
ex
x
-a（x2-2x-3），其中a为参数，且a∈R．
（Ⅰ）若a=-1，求f（x）的单调区间；
（Ⅱ）若对于任意的x∈（0，4]，都有f（x）≥0恒成立，求参数a的取值范围．
若（ax2-
1
x
）9的展开式中常项等于84，则实数a=
 
（用数字作答）．
已知a 
1
2
+a-
1
2
=3（a＞0），求
a
3
2
-a-
3
2
a
1
2
-a-
1
2
的值．
已知集合A={x|x=2n，n∈Z}，B={x|x=2n+1，n∈Z}，i是虚数单位，若k∈Z且ik∈{-1，1}，则（　　）
A、k∈AB、k∈B
C、k∈A∩BD、k∈∅

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网