题目内容
已知函数f(x)=
,若存在k使得函数f(x)的值域是[0,2],则实数a的取值范围是( )
|
A、[
| ||
B、[1,
| ||
C、(0,
| ||
| D、{2} |
考点:分段函数的应用
专题:计算题,数形结合,函数的性质及应用
分析:由于y=log2(1-x)+1在[-1,k)上是递减函数,再由函数f(x)的值域是[0,2],得到k的范围,
再由y=x3-3x+2的图象,结合函数的值域[0,2],从而得到a的取值范围.
再由y=x3-3x+2的图象,结合函数的值域[0,2],从而得到a的取值范围.
解答:
 解:由于y=log2(1-x)+1在[-1,k)上是递减函数,
解:由于y=log2(1-x)+1在[-1,k)上是递减函数,
且x=-1时,y=2,x=
时,y=0,故-1<k≤
,
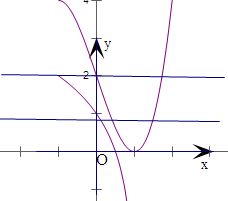
画出函数f(x)的图象,令x3-3x+2=2,解得x=0,
,-
(舍去),由于存在k使得函数f(x)的值域是[0,2],
故a的取值范围是[1,
].
故选B.
 解:由于y=log2(1-x)+1在[-1,k)上是递减函数,
解:由于y=log2(1-x)+1在[-1,k)上是递减函数,且x=-1时,y=2,x=
| 1 |
| 2 |
| 1 |
| 2 |
画出函数f(x)的图象,令x3-3x+2=2,解得x=0,
| 3 |
| 3 |
故a的取值范围是[1,
| 3 |
故选B.
点评:本题考查分段函数的图象和应用,考查函数的单调性和值域,考查数形结合的能力,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
过点P(0,5)的直线l被圆C:x2+y2+4x-12y+24=0所截得的线段长4
,则l的方程为( )
| 3 |
| A、3x-4y+20=0或x=0 |
| B、3x-4y+20=0 |
| C、x=0 |
| D、4x-3y+20=0 |
定义:平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)称为平面斜坐标系;在平面斜坐标系xOy中,若
=xe1+ye2(其中e1、e2分别是斜坐标系x轴、y轴正方向上的单位向量,x,y∈R,O为坐标系原点),则有序数对(x,y)称为点P的斜坐标.在平面斜坐标系xOy中,若∠xOy=120°,点A的斜坐标为(5,3),直线l过点A且其向上方向与x轴正方向之间所成的角为60°,则直线l在斜坐标系xOy中的方程是( )
| OP |
| A、x-y+2=0 | ||||
| B、x-y-2=0 | ||||
C、
| ||||
D、x-
|
若四边ABCD满足
+
=
,(
-
)•
=0,则该四边形是( )
| AB |
| CD |
| 0 |
| AB |
| DB |
| AB |
| A、菱形 | B、矩形 |
| C、直角梯形 | D、正方形 |
已知集合M={x|x=1+a2,a∈N*},P={x|x=a2-4a+5,a∈N*},则M与P的关系为( )
| A、M?P | B、P?M |
| C、M⊆P | D、M?P |
