题目内容
已知点P(-2,-3),圆C:(x-4)2+(y-2)2=9,过P点作圆C的两条切线,切点分别为A、B
(1)求过P、A、B三点的外接圆的方程;
(2)求直线AB的方程.
(1)求过P、A、B三点的外接圆的方程;
(2)求直线AB的方程.
考点:圆的一般方程,直线的一般式方程
专题:计算题,直线与圆
分析:(1)连结CA、CB.由平面几何知, CA⊥PA,CB⊥PB.这些点P、A、C、B共圆,且CP为直径.这也是过三点A、B、PP的圆;
(2)由x2+y2-2x+y-14=0与(x-4)2+(y-2)2=9相减,得直线AB的方程.
(2)由x2+y2-2x+y-14=0与(x-4)2+(y-2)2=9相减,得直线AB的方程.
解答:
 解:(1)如图所示,连结CA、CB.由平面几何知, CA⊥PA,CB⊥PB.这些点P、A、C、B共圆,且CP为直径.这也是过三点A、B、PP的圆.
解:(1)如图所示,连结CA、CB.由平面几何知, CA⊥PA,CB⊥PB.这些点P、A、C、B共圆,且CP为直径.这也是过三点A、B、PP的圆.
∵P(-2,-3),圆心坐标为C(4,2),?
∴所求圆的方程为(x+2)(x-4)+(y+3)( y-2)=0,即x2+y2-2x+y-14=0.
(2)直线AB即为这两个圆的公共弦所在直线.
由x2+y2-2x+y-14=0与(x-4)2+(y-2)2=9相减,得6x+5y-25=0.
 解:(1)如图所示,连结CA、CB.由平面几何知, CA⊥PA,CB⊥PB.这些点P、A、C、B共圆,且CP为直径.这也是过三点A、B、PP的圆.
解:(1)如图所示,连结CA、CB.由平面几何知, CA⊥PA,CB⊥PB.这些点P、A、C、B共圆,且CP为直径.这也是过三点A、B、PP的圆.∵P(-2,-3),圆心坐标为C(4,2),?
∴所求圆的方程为(x+2)(x-4)+(y+3)( y-2)=0,即x2+y2-2x+y-14=0.
(2)直线AB即为这两个圆的公共弦所在直线.
由x2+y2-2x+y-14=0与(x-4)2+(y-2)2=9相减,得6x+5y-25=0.
点评:本题考查圆的方程,考查学生的计算能力,正确求出过P、A、B三点的外接圆的方程是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在等比数列{an}中,a2+a3+…+a8=8,
+
+…+
=2,则a5的值( )
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a8 |
| A、±2 | B、2 | C、±3 | D、3 |
已知函数f(x)=
,若存在k使得函数f(x)的值域是[0,2],则实数a的取值范围是( )
|
A、[
| ||
B、[1,
| ||
C、(0,
| ||
| D、{2} |
 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.
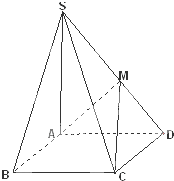 如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥底面ABCD,M为SD的中点,且SA=AD=2AB.
如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥底面ABCD,M为SD的中点,且SA=AD=2AB.