题目内容
已知数列{an},{bn},a1=1,an=an-1+2n-1,bn=
,Sn为数列{bn}的前n项和,Tn为数列{Sn}的前n项和.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{bn}的前n项和Sn;
(Ⅲ)求证:Tn>
-
.
| an-1+1 |
| anan+1 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{bn}的前n项和Sn;
(Ⅲ)求证:Tn>
| n |
| 2 |
| 1 |
| 3 |
考点:数列的求和
专题:综合题,等差数列与等比数列
分析:(Ⅰ)利用叠加法,求数列{an}的通项公式;
(Ⅱ)利用裂项法,求数列{bn}的前n项和Sn;
(Ⅲ)利用放缩法,再结合等比数列的求和公式,即可证明.
(Ⅱ)利用裂项法,求数列{bn}的前n项和Sn;
(Ⅲ)利用放缩法,再结合等比数列的求和公式,即可证明.
解答:
(Ⅰ)解:∵an=an-1+2n-1,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=2n-1 …(5分)
(Ⅱ)解:bn=
=
(
-
),
∴Sn=
[(
-
)+(
-
)+…+(
-
)]=
(1-
)=
…(10分)
(Ⅲ)证明:∵Sn=
-
≥
-
•
,
∴Tn≥
-
(
+
+…+
)=
-
(1-
)>
-
.…(14分)
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=2n-1 …(5分)
(Ⅱ)解:bn=
| an-1+1 |
| anan+1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
∴Sn=
| 1 |
| 2 |
| 1 |
| 2-1 |
| 1 |
| 22-1 |
| 1 |
| 22-1 |
| 1 |
| 23-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
| 1 |
| 2 |
| 1 |
| 2n+1-1 |
| 2n-1 |
| 2n+1-1 |
(Ⅲ)证明:∵Sn=
| 1 |
| 2 |
| 1 |
| 3•2k+2k-2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2k |
∴Tn≥
| n |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| n |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n |
| n |
| 2 |
| 1 |
| 3 |
点评:本题考查数列与不等式的综合,考查叠加法,裂项法、放缩法的运用,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
,若存在k使得函数f(x)的值域是[0,2],则实数a的取值范围是( )
|
A、[
| ||
B、[1,
| ||
C、(0,
| ||
| D、{2} |

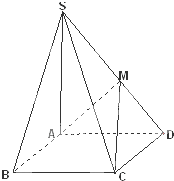 如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥底面ABCD,M为SD的中点,且SA=AD=2AB.
如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥底面ABCD,M为SD的中点,且SA=AD=2AB.