题目内容
过双曲线
-
=1(a>0,b>0)的左焦点F(-c,0)作圆(x-c)2+y2=c2的切线,切点为E,且该切线与双曲线的右支交于点A.若
=
(
+
),则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| OE |
| 1 |
| 2 |
| OF |
| OA |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:FE是圆F′:(x-c)2+y2=c2的切线,可得F′E⊥EF,利用勾股定理可得EF=
=
c.由于
=
(
+
),可得点E是线段AF的中点,于是|AF|=2
c,|AF′|=|FF′|=2c.再利用双曲线的定义即可得出.
| |FF′|2-|EF′|2 |
| 3 |
| OE |
| 1 |
| 2 |
| OF |
| OA |
| 3 |
解答:
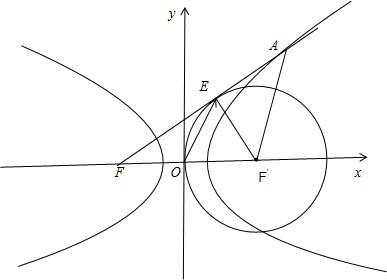 解:如图所示,
解:如图所示,
∵FE是圆F′:(x-c)2+y2=c2的
切线,
∴F′E⊥EF,
∴EF=
=
c.
∵
=
(
+
),
∴点E是线段AF的中点,
∴|AF|=2
c,|AF′|=|FF′|=2c.
∵|AF|-|AF′|=2a,
∴2
c-2c=2a,
∴
=
=
+1.
故选:C.
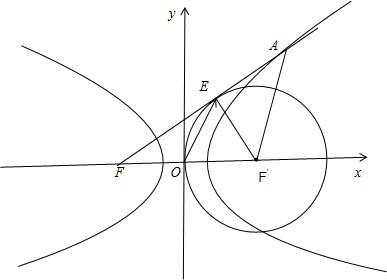 解:如图所示,
解:如图所示,∵FE是圆F′:(x-c)2+y2=c2的
切线,
∴F′E⊥EF,
∴EF=
| |FF′|2-|EF′|2 |
| 3 |
∵
| OE |
| 1 |
| 2 |
| OF |
| OA |
∴点E是线段AF的中点,
∴|AF|=2
| 3 |
∵|AF|-|AF′|=2a,
∴2
| 3 |
∴
| c |
| a |
| 1 | ||
|
| 3 |
故选:C.
点评:本题考查了双曲线的定义及其性质、直线与圆相切的性质、勾股定理、等腰三角形的性质,考查了推理能力与计算能力.

练习册系列答案
相关题目
已知角α的终边与单位圆交于P(-
,
),则cos(α-
)的值为( )
| 1 |
| 2 |
| ||
| 2 |
| π |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
过点P(1,1)的直线l交圆C:x2+y2=8于A,B两点,O为坐标原点且∠AOB=120°,则直线l的方程为( )
| A、y=-2x+3 |
| B、y=-x+2 |
| C、y=x |
| D、y=2x-1 |
函数y=2sin(2x-
)的一条对称轴是( )
| π |
| 4 |
A、x=
| ||
B、x=
| ||
C、x=-
| ||
D、x=
|
已知{an}是等比数列,a2=2,a3=
,则公比q=( )
| 1 |
| 4 |
A、-
| ||
| B、-2 | ||
| C、2 | ||
D、
|
在△ABC中,a、b、c分别为角A、B、C的对边,且b=3,c=3
,A=30°,则a=( )
| 3 |
| A、6 | B、3 | C、6或3 | D、6或4 |
下列各式中与排列数A
相等的是( )
m n |
A、
| ||||
| B、n(n-1)(n-2)…(n-m) | ||||
C、
| ||||
D、A
|
f(x)=ax-1的图象过点(4,2),用f-1(x)表示f(x)的反函数,则f-1(2)=( )
A、-
| ||
B、
| ||
| C、2 | ||
| D、4 |