题目内容
过点P(1,1)的直线l交圆C:x2+y2=8于A,B两点,O为坐标原点且∠AOB=120°,则直线l的方程为( )
| A、y=-2x+3 |
| B、y=-x+2 |
| C、y=x |
| D、y=2x-1 |
考点:直线与圆的位置关系
专题:直线与圆
分析:根据题意画出图象,根据图象得到△AOB为等腰三角形,过点O作OC垂直于直线AB,得到三角形AOP为直角三角形,且角OAP=30°,进而得到|OP|=
|OA|,而线段OA为圆的半径2
,所以得到线段OP的长,然后利用点到直线的距离公式表示出圆心O到所设直线的距离d,让d等于线段OP的长,列出关于k的方程,求出方程的解即可得到k的值且得到此时的点C即为点P,写出直线l的方程即可.
| 1 |
| 2 |
| 2 |
解答:
解:由题意画出图象,如图所示: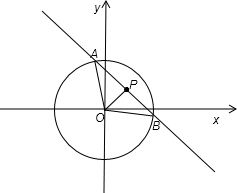
由∠AOB=120°,OA=OB,得到△AOB为等腰三角形,
∴∠OAB=30°,过点O作OC⊥直线AB,垂足为点C,
设直线AB的方程为:y-1=k(x-1),即kx-y+1-k=0,
则|OC|=
=
|OA|=
,化简得:(k+1)2=0,
解得:k=-1,又|OP|=
,且此时点C即为点P,
所以直线l的方程为:x+y-2=0,即y=-x+2.
故选:B.

由∠AOB=120°,OA=OB,得到△AOB为等腰三角形,
∴∠OAB=30°,过点O作OC⊥直线AB,垂足为点C,
设直线AB的方程为:y-1=k(x-1),即kx-y+1-k=0,
则|OC|=
| |1-k| | ||
|
| 1 |
| 2 |
| 2 |
解得:k=-1,又|OP|=
| 2 |
所以直线l的方程为:x+y-2=0,即y=-x+2.
故选:B.
点评:此题考查学生掌握直线与圆相交的性质,灵活运用点到直线的距离公式化简求值,考查了数形结合的数学思想,是一道中档题.

练习册系列答案
相关题目
同时掷两个大小相同的硬币,出现一正一反的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
数列{an}是等比数列,则下列结论中正确的是( )
| A、对任意k∈N*,都有akak+1>0 |
| B、对任意k∈N*,都有akak+1ak+2>0 |
| C、对任意k∈N*,都有akak+2>0 |
| D、对任意k∈N*,都有akak+2ak+4>0 |
函数f(x)是定义域为R的偶函数,当x>0时f(x)=-x+1,则当x<0时,f(x)的表达式为( )
| A、f(x)=-x+1 |
| B、f(x)=-x-1 |
| C、f(x)=x+1 |
| D、f(x)=x-1 |
方程f(x)=x的根称为函数f(x)的不动点,若函数f(x)=
有唯一不动点,且x1=1000,xn+1=
,n为正整数,则x2011=( )
| x |
| a(x+2) |
| 1 | ||
f(
|
| A、2005 | B、2006 |
| C、2007 | D、2008 |
过双曲线
-
=1(a>0,b>0)的左焦点F(-c,0)作圆(x-c)2+y2=c2的切线,切点为E,且该切线与双曲线的右支交于点A.若
=
(
+
),则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| OE |
| 1 |
| 2 |
| OF |
| OA |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
α,β,γ为不同的平面,m,n,l为不同的直线,则m⊥β的一个充分条件是( )
| A、n⊥α,n⊥β,m⊥α |
| B、α∩γ=m,α⊥γ,β⊥γ |
| C、α⊥γ,β⊥γ,m⊥α |
| D、α⊥β,α∩β=l,m⊥l |