题目内容
已知复数z满足（1+i）z=1-i，其中i为虚数单位，则|z|= ．
考点：复数求模
专题：数系的扩充和复数
分析：由（1+i）z=1-i可求得z=
，两端取模即可．
| 1-i |
| 1+i |
解答：
解：∵（1+i）z=1-i，
∴z=
，
∴|z|=
=
=1，
故答案为：1．
∴z=
| 1-i |
| 1+i |
∴|z|=
| |1-i| |
| |1+i| |
| ||
|
故答案为：1．
点评：本题考查复数的模的运算性质，属于基础题．
练习册系列答案
相关题目
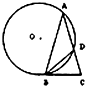如图，△ABC中AB=AC，∠ABC=72°，圆O过A，B且与BC切于B点，与AC交于D点，连BD．若BC=2，则AC=
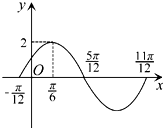函数y=2sin（ωx+φ）（ω＞0，|φ|＜
一个三棱锥的三视图如图所示，其正视图、左视图、俯视图的面积分别是1，2，4，则这个三棱锥的表面积为