题目内容
已知四数a1，a2，a3，a4依次成等比数列，且公比q不为1．将此数列删去一个数后得到的数列（按原来的顺序）是等差数列，则正数q的取值集合是 ．
考点：等差数列的性质
专题：综合题,等差数列与等比数列
分析：因为公比q不为1，所以不能删去a1，a4．设{an}的公差为d，分类讨论，即可得出结论．
解答：
解：因为公比q不为1，所以不能删去a1，a4．设{an}的公差为d，则
①若删去a2，则由2a3=a1+a4得2a1q2=a1+a1q3，即2q2=1+q3，
整理得q2（q-1）=（q-1）（q+1）．
又q≠1，则可得 q2=q+1，又q＞0解得q=
；
②若删去a3，则由2a2=a1+a4得2a1q=a1+a1q3，即2q=1+q3，整理得q（q-1）（q+1）=q-1．
又q≠1，则可得q（q+1）=1，又q＞0解得 q=
．
综上所述，q=
．
故答案为：{
，
}．
①若删去a2，则由2a3=a1+a4得2a1q2=a1+a1q3，即2q2=1+q3，
整理得q2（q-1）=（q-1）（q+1）．
又q≠1，则可得 q2=q+1，又q＞0解得q=
1+
| ||
| 2 |
②若删去a3，则由2a2=a1+a4得2a1q=a1+a1q3，即2q=1+q3，整理得q（q-1）（q+1）=q-1．
又q≠1，则可得q（q+1）=1，又q＞0解得 q=
-1+
| ||
| 2 |
综上所述，q=
±1+
| ||
| 2 |
故答案为：{
-1+
| ||
| 2 |
1+
| ||
| 2 |
点评：本题主要考查等差数列等差中项的概念及等比数列中基本量的运算．
练习册系列答案
名校课堂系列答案
相关题目
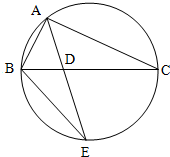如图所示，圆的两条弦AE，BC交于点D，且