Question

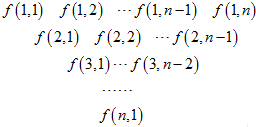一个三角形数表按如下方式构成（如图：其中项数n≥5）：第一行是以4为首项，4为公差的等差数列，从第二行起，每一个数是其肩上两个数的和，例如：f（2，1）=f（1，1）+f（1，2）；f（i，j）为数表中第i行的第j个数．
（1）求第2行和第3行的通项公式f（2，j）和f（3，j）；
（2）证明：数表中除最后2行外每一行的数都依次成等差数列，并求f（i，1）关于i（i=1，2，…，n）的表达式；
（3）若f（i，1）=（i+1）（a_i-1），b_i=

1

aiai+1

，试求一个等比数列g（i）（i=1，2，…，n），使得S_n=b₁g（1）+b₂2g（2）+…+b_ng（n）＜

1

3

，且对于任意的m∈（

1

4

，

1

3

）均存在实数λ，当n＞λ时，都有S_n＞m．

Answer 1

考点：等差数列与等比数列的综合,数列的应用

专题：等差数列与等比数列

分析：（1）根据等差数列和等比数列的定义即可求出相应的通项公式，
（2）根据条件建立方程关系即可求出f（i，1）的表达式．
（3）根据条件寻找等比数列g（i），即可得到结论．

解答： 解：（1）f（2，j）=f（1，j）+f（1，j+1）=2f（1，j）+4=8j+4（j=1，2，…，n-1）
f（3，j）=f（2，j）+f（2，j+1）=2f（2，j）+8=2（8j+4）+8=16j+16（j=1，2，…，n-2）．
（2）由已知，第一行是等差数列，假设第i（1≤i≤n-3）行是以d_i为公差的等差数列，
则由f（i+1，j+1）-f（i+1，j）=[f（i，j+1）+f（i，j+2）]-[f（i，j）+f（i，j+1）]=f（i，j+2）-f（i，j）=2d_i（常数）知第i+1（1≤i≤n-3）行的数也依次成等差数列，且其公差为2d_i．综上可得，数表中除最后2行以外每一行都成等差数列；
由于d₁=4，d_i=2d_i-1（i≥2），
∴di=4•2i-1=2i+1，
即f（i，1）=f（i-1，1）+f（i-1，2）=2f（i-1，1）+d_i-1，由di-1=2i，
得f（i，1）=2f（i-1，1）+2ⁱ，
于是

f(i，1)

2i

=

f(i-1，1)

2i-1

+1，
即

f(i，1)

2i

-

f(i-1，1)

2i-1

=1，
又∵

f(1，1)

21

=

4

2

=2，
∴数列{

f(i，1)

2i

}是以2为首项，1为公差的等差数列，
∴

f(i，1)

2i

=2+(i-1)=i+1，∴f（i，1）=（i+1）•2ⁱ（i=1，2，…，n）．  
（3）f（i，1）=（i+1）（a_i-1）⇒ai=

f(i，1)

i+1

+1=2i+1，⇒bi=

1

aiai+1

=

1

(2i+1+1)(2i+1)

=

1

2i

(

1

2i+1

-

1

2i+1+1

)，
令g（i）=2ⁱ⇒big(i)=

1

2i

(

1

2i+1

-

1

2i+1+1

)×2i=

1

2i+1

-

1

2i+1+1

，
⇒Sn=(

1

2+1

-

1

22+1

)+(

1

22+1

-

1

23+1

)+…+(

1

2n+1

-

1

2n+1+1

)=

1

3

-

1

2n+1+1

＜

1

3

．
S_n＞m?

1

3

-

1

2n+1+1

＞m?

1

2n+1+1

＜

1

3

-m=

1-3m

3

，m∈(

1

4

，

1

3

)⇒0＜1-3m＜

1

4

，⇒2n+1+1＞

3

1-3m

⇒n＞log2(

3

1-3m

-1)-1，
令λ=log2(

3

1-3m

-1)，
则当n＞λ时，都有S_n＞m，∴适合题设的一个等比数列为g（i）=2ⁱ．

点评：本题主要考查等差数列和等比数列的综合应用，考查学生的运算能力，综合性较强，运算量较大．