题目内容
在莫言获得诺贝尔奖后，某高校在男、女生中各抽取50名，调查对莫言作品的了解程度，统计结果如下表所示：
（Ⅰ）试估计该校学生阅读莫言作品不低于50篇的概率；
（Ⅱ）若对莫言作品阅读低于50篇称为对莫言作品“一般了解”，否则称为对莫言作品“非常了解”，根据题意完成下表，并判断对莫言作品的了解程度是否与性别有关．
参考数据及公式如下：
K2=
．
| 阅读过莫言作品的作品是（篇） | [0，25） | [25，50） | [50，75） | [75，100） | [100，125） |
| 男生人数 | 6 | 12 | 18 | 10 | 4 |
| 女生人数 | 4 | 16 | 16 | 13 | 1 |
（Ⅱ）若对莫言作品阅读低于50篇称为对莫言作品“一般了解”，否则称为对莫言作品“非常了解”，根据题意完成下表，并判断对莫言作品的了解程度是否与性别有关．
| 一般了解 | 非常了解 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P（K2≥k） | 0.05 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
考点：独立性检验的应用
专题：计算题,概率与统计
分析：（Ⅰ）求出阅读莫言作品在50篇以上的频率，估计该校学生阅读莫言作品超过50篇的概率；
（Ⅱ）利用独立性检验的知识进行判断．
（Ⅱ）利用独立性检验的知识进行判断．
解答：
解：（Ⅰ）由抽样调查阅读莫言作品在50篇以上的频率为
=
，
据此估计该校学生阅读莫言作品超过50篇的概率约为P=
…..（5分）
（Ⅱ）
…..（8分）
根据列联表数据得，K2=
≈0.169＜3.843
所以说没有足够的把握说对莫言作品的了解与性别有关…（12分）
| 32+30 |
| 100 |
| 31 |
| 50 |
据此估计该校学生阅读莫言作品超过50篇的概率约为P=
| 31 |
| 50 |
（Ⅱ）
| 非常了解 | 一般了解 | 合计 | |
| 男生 | 32 | 18 | 50 |
| 女生 | 30 | 20 | 50 |
| 合计 | 62 | 38 | 100 |
根据列联表数据得，K2=
| 100×(32×20-30×18)2 |
| 50×50×62×38 |
所以说没有足够的把握说对莫言作品的了解与性别有关…（12分）
点评：本题主要考查独立性检验的应用，利用列联表计算出K2，是解决本题的关键．这类题目主要是通过计算数据来进行判断的．
练习册系列答案
相关题目
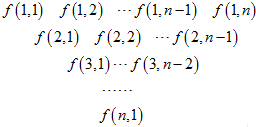一个三角形数表按如下方式构成（如图：其中项数n≥5）：第一行是以4为首项，4为公差的等差数列，从第二行起，每一个数是其肩上两个数的和，例如：f（2，1）=f（1，1）+f（1，2）；f（i，j）为数表中第i行的第j个数．
在椭圆C：
如图，在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=AA1．若D为B1C1的中点，求直线AD与平面A1BC1所成的角．