题目内容
已知F1，F2是双曲线
-
=1（a＞0，b＞0）的左右两个焦点，过点F1作垂直于x轴的直线与双曲线的两条渐近线分别交于A，B两点，△ABF2是锐角三角形，则该双曲线的离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、（1，2） | ||
B、（1，
| ||
| C、（1，5） | ||
D、（
|
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据题意，求出AB=
，F1F2=2c，△ABF2是锐角三角形，只要∠AF2B为锐角，即AF1＜F1F2即可，从而可得结论．
| 2bc |
| a |
解答：
解：根据题意，易得AB=
，F1F2=2c，
由题设条件可知△ABF2为等腰三角形，
△ABF2是锐角三角形，只要∠AF2B为锐角，即AF1＜F1F2即可；
所以有
＜2c，
即4a2＞c2-a2，
解出e∈（1，
），
故选：B．
| 2bc |
| a |
由题设条件可知△ABF2为等腰三角形，
△ABF2是锐角三角形，只要∠AF2B为锐角，即AF1＜F1F2即可；
所以有
| bc |
| a |
即4a2＞c2-a2，
解出e∈（1，
| 5 |
故选：B．
点评：本题考查双曲线的离心率和锐角三角形的判断，在解题过程中要注意隐含条件的挖掘．
练习册系列答案
星级口算天天练系列答案
相关题目
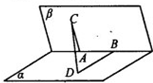如图，在二面角α-AB-β的棱上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直于AB，已知AB=4，AC=6，BD=8，CD=2| 17 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设F（x）=f（x）+f（-x），且f′（x）存在，则F′（x）是（ ）
| A、奇函数 |
| B、偶函数 |
| C、非奇非偶的函数 |
| D、不能判定其奇偶性的函数 |
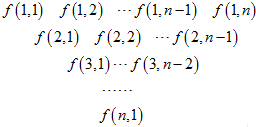一个三角形数表按如下方式构成（如图：其中项数n≥5）：第一行是以4为首项，4为公差的等差数列，从第二行起，每一个数是其肩上两个数的和，例如：f（2，1）=f（1，1）+f（1，2）；f（i，j）为数表中第i行的第j个数．