题目内容
在平面直角坐标系中,O为坐标原点,抛物线y2=x的弦PQ被直线L:x+y-2=0垂直平分,求△OPQ的面积.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:设出P,Q的坐标,把PQ中点M的坐标用P,Q的坐标表示,由M在L上得P,Q坐标的关系,再由PQ得斜率等于1得P,Q坐标的另一关系,联立方程组求得P,Q的坐标,求出OP,OQ的长度,判断出OP与OQ垂直,然后代入三角形的面积公式求面积.
解答:
解:设P(a,a2),Q(b,b2),中点M(
,
)
将M代入L:x+y-2=0,得
+
-2=0,即a+b+a2+b2=4 ①.
又PQ垂直L,
∴kPQ=1,即
=1,a+b=1 ②.
代入①得:a2-a-1=0,解得:a=
.
当a=
时,b=
.
当a=
时,b=
.
∴P(
,
),Q(
,
),或P(
,
),Q(
,
).
∵
•
+
•
=0,
∴OP⊥OQ,
当P(
,
),Q(
,
)时,|OP|=
=
,|OQ|=
=
.
∴S△OPQ=
×
×
=
.
当P(
,
),Q(
,
)时,同理可得S△OPQ=
.
| a+b |
| 2 |
| a2+b2 |
| 2 |
将M代入L:x+y-2=0,得
| a+b |
| 2 |
| a2+b2 |
| 2 |
又PQ垂直L,
∴kPQ=1,即
| a2-b2 |
| a-b |
代入①得:a2-a-1=0,解得:a=
1±
| ||
| 2 |
当a=
1+
| ||
| 2 |
1-
| ||
| 2 |
当a=
1-
| ||
| 2 |
1+
| ||
| 2 |
∴P(
1+
| ||
| 2 |
3+
| ||
| 2 |
1-
| ||
| 2 |
3-
| ||
| 2 |
1-
| ||
| 2 |
3-
| ||
| 2 |
1+
| ||
| 2 |
3+
| ||
| 2 |
∵
1-
| ||
| 2 |
1+
| ||
| 2 |
3-
| ||
| 2 |
3+
| ||
| 2 |
∴OP⊥OQ,
当P(
1+
| ||
| 2 |
3+
| ||
| 2 |
1-
| ||
| 2 |
3-
| ||
| 2 |
(
|
5+2
|
(
|
5-2
|
∴S△OPQ=
| 1 |
| 2 |
5+2
|
5-2
|
| ||
| 2 |
当P(
1-
| ||
| 2 |
3-
| ||
| 2 |
1+
| ||
| 2 |
3+
| ||
| 2 |
| ||
| 2 |
点评:本题是直线与圆锥曲线的综合题,解答的关键是充分利用抛物线y2=x的弦PQ被直线L:x+y-2=0垂直平分列P,Q坐标的关系,从而求得P,Q的坐标,考查了计算能力,是中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
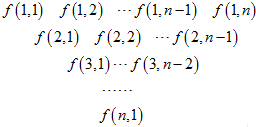 一个三角形数表按如下方式构成(如图:其中项数n≥5):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:f(2,1)=f(1,1)+f(1,2);f(i,j)为数表中第i行的第j个数.
一个三角形数表按如下方式构成(如图:其中项数n≥5):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:f(2,1)=f(1,1)+f(1,2);f(i,j)为数表中第i行的第j个数. 一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样本,称出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的重量频率分布直方图,如图.
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样本,称出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的重量频率分布直方图,如图. 在椭圆C:
在椭圆C: 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.若D为B1C1的中点,求直线AD与平面A1BC1所成的角.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.若D为B1C1的中点,求直线AD与平面A1BC1所成的角.