题目内容
已知∠A的终边上一点P（15a，8a）（a∈R，且a≠0），求∠A的三个三角函数值．
考点：任意角的三角函数的定义
专题：三角函数的求值
分析：由两点间的距离公式，算出|OP|，再三角函数的定义加以计算，可得∠A的三个三角函数值．
解答：
解：∵a∈R，且a≠0，点P（15a，8a），
∴r=|OP|=
=17|a|，
a＞0时，可得cos∠A=
=
，
sin∠A=
，
tan∠A=
；
当a＜0时，cos∠A=
=-
，
sin∠A=-
，
tan∠A=
；
∴r=|OP|=
| (15a)2+(8a)2 |
a＞0时，可得cos∠A=
| 15a |
| 17|a| |
| 15 |
| 17 |
sin∠A=
| 8 |
| 17 |
tan∠A=
| 8 |
| 15 |
当a＜0时，cos∠A=
| 15a |
| 17|a| |
| 15 |
| 17 |
sin∠A=-
| 8 |
| 17 |
tan∠A=
| 8 |
| 15 |
点评：本题给出角α的终边上一点P的坐标，求∠A的三角函数值．着重考查了两点间的距离公式和任意角的三角函数的定义等知识，属于基础题．
练习册系列答案
相关题目
设F（x）=f（x）+f（-x），且f′（x）存在，则F′（x）是（ ）
| A、奇函数 |
| B、偶函数 |
| C、非奇非偶的函数 |
| D、不能判定其奇偶性的函数 |
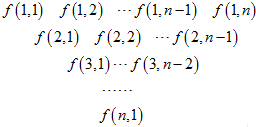一个三角形数表按如下方式构成（如图：其中项数n≥5）：第一行是以4为首项，4为公差的等差数列，从第二行起，每一个数是其肩上两个数的和，例如：f（2，1）=f（1，1）+f（1，2）；f（i，j）为数表中第i行的第j个数．
一个盒子中装有大量形状大小一样但重量不尽相同的小球，从中随机抽取50个作为样本，称出它们的重量（单位：克），重量分组区间为（5，15]，（15，25]，（25，35]，（35，45]，由此得到样本的重量频率分布直方图，如图．