题目内容
已知函数y=lgx•lg(ax)(
≤x≤10)的最小值为2,求a的值.
| 1 |
| 10 |
考点:对数的运算性质
专题:函数的性质及应用
分析:利用换元法,根据对数的运算性质,将函数转化为关于t的一元二次函数,利用一元二次函数对称轴与区间的关系,即可得到结论.
解答:
解:y=lgx•lg(ax)=y=lgx•(lgx+lga)=lg2x+lga•lgx,
设t=lgx,则函数等价为y=g(t)=t2+lga•t,
∵
≤x≤10,
∴-1≤lgx≤1,即-1≤t≤1,
函数的对称轴为x=-
,
若-
≤-1,即lga≥2时,最小值为g(-1)=1-lga=2,
∴lga=-1,此时不成立.
若-
≥-1,即lga≤2时,最小值为g(1)=1+lga=2,
解得lga=1,此时a=10.
设t=lgx,则函数等价为y=g(t)=t2+lga•t,
∵
| 1 |
| 10 |
∴-1≤lgx≤1,即-1≤t≤1,
函数的对称轴为x=-
| lga |
| 2 |
若-
| lga |
| 2 |
∴lga=-1,此时不成立.
若-
| lga |
| 2 |
解得lga=1,此时a=10.
点评:本题主要考查对数的基本运算以及二次函数的图象和性质,利用换元法是解决本题的关键.

练习册系列答案
相关题目
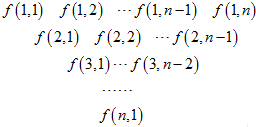 一个三角形数表按如下方式构成(如图:其中项数n≥5):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:f(2,1)=f(1,1)+f(1,2);f(i,j)为数表中第i行的第j个数.
一个三角形数表按如下方式构成(如图:其中项数n≥5):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:f(2,1)=f(1,1)+f(1,2);f(i,j)为数表中第i行的第j个数. 在椭圆C:
在椭圆C: