题目内容
已知函数f(x)=x3-3ax2+b(x∈R),其中a≠0,b∈R.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设a∈[
,
],函数f(x)在区间[1,2]上的最大值为M,最小值为m,求M-m的取值范围.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设a∈[
| 1 |
| 2 |
| 3 |
| 4 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)对于含参数的函数f(x)的单调区间的求法,需要进行分类讨论,然后利用导数求出函数的单调性;
(Ⅱ)求出f(x)在[1,2a]内是减函数,在[2a,2]内是增函数,设 g(a)=4a3-12a+8,求出g(a)在[
,
]内是减函数,问题得以解决.
(Ⅱ)求出f(x)在[1,2a]内是减函数,在[2a,2]内是增函数,设 g(a)=4a3-12a+8,求出g(a)在[
| 1 |
| 2 |
| 3 |
| 4 |
解答:
解:(Ⅰ)f'(x)=3x2-6ax=3x(x-2a),令f'(x)=0,则x1=0,x2=2a,
(1)当a>0时,0<2a,当x变化时,f'(x),f(x)的变化情况如下表:
∴函数f(x)在区间(-∞,0)和(2a,+∞)内是增函数,在区间(0,2a)内是减函数.
(2)当a<0时,2a<0,当x变化时,f'(x),f(x)的变化情况如下表:
∴函数f(x)在区间(-∞,2a)和(0,+∞)内是增函数,在区间(2a,0)内是减函数.
(Ⅱ)由
≤a≤
及(Ⅰ),f(x)在[1,2a]内是减函数,在[2a,2]内是增函数,
又f(2)-f(1)=(8-12a+b)-(1-3a+b)=7-9a>0,
∴M=f(2),m=f(2a)=8a3-12a3+b=b-4a3,
∴M-m=(8-12a+b)-(b-4a3)=4a3-12a+8,
设 g(a)=4a3-12a+8,
∴g'(a)=12a2-12=12(a+1)(a-1)<0(a∈[
,
]),
∴g(a)在[
,
]内是减函数,
故 g(a)max=g(
)=2+
=
,g(a)min=g(
)=-1+4×
=
.
∴
≤M-m≤
.
(1)当a>0时,0<2a,当x变化时,f'(x),f(x)的变化情况如下表:
| x | (-∞,0) | 0 | (0,2a) | 2a | (2a,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
(2)当a<0时,2a<0,当x变化时,f'(x),f(x)的变化情况如下表:
| x | (-∞,2a) | 2a | (2a,0) | 0 | (0,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
(Ⅱ)由
| 1 |
| 2 |
| 3 |
| 4 |
又f(2)-f(1)=(8-12a+b)-(1-3a+b)=7-9a>0,
∴M=f(2),m=f(2a)=8a3-12a3+b=b-4a3,
∴M-m=(8-12a+b)-(b-4a3)=4a3-12a+8,
设 g(a)=4a3-12a+8,
∴g'(a)=12a2-12=12(a+1)(a-1)<0(a∈[
| 1 |
| 2 |
| 3 |
| 4 |
∴g(a)在[
| 1 |
| 2 |
| 3 |
| 4 |
故 g(a)max=g(
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 3 |
| 4 |
| 33 |
| 42 |
| 11 |
| 16 |
∴
| 11 |
| 16 |
| 5 |
| 2 |
点评:本题考查利用导数研究函数的极值和单调性,涉及构造函数的方法,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
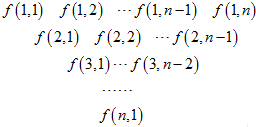 一个三角形数表按如下方式构成(如图:其中项数n≥5):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:f(2,1)=f(1,1)+f(1,2);f(i,j)为数表中第i行的第j个数.
一个三角形数表按如下方式构成(如图:其中项数n≥5):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:f(2,1)=f(1,1)+f(1,2);f(i,j)为数表中第i行的第j个数. 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.若D为B1C1的中点,求直线AD与平面A1BC1所成的角.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.若D为B1C1的中点,求直线AD与平面A1BC1所成的角.