题目内容

已知平面直角坐标系中
OA
=（2
2
，0），满足
OB
+
OA
=
0
，平面内有一动点E使得|
BE
-
BA
|+|
AE
-
AB
|=6．
（1）求动点E的轨迹方程C；
（2）过曲线C上的动点P向圆x2+y2=1引切线PA，PB，其中A，B为切点且直线AB交x轴，y轴于M，N，求△MON面积的最小值．
考点：直线与圆锥曲线的综合问题
专题：向量与圆锥曲线
分析：（1）由已知向量的坐标和向量等式求出
OB
的坐标，再由|
BE
-
BA
|+|
AE
-
AB
|=6得到|
AE
|+|
BE
|=6．由此可知动点E的轨迹为椭圆，结合椭圆定义求得椭圆方程；
（2）设出P点坐标，得到以|OP|为直径的圆的方程，与已知圆的方程联立得到过切点A，B的直线方程，求得直线与坐标轴的交点，由两点间的距离公式求得MN的距离，再由点到直线的距离公式求得O到MN的距离，代入三角形的面积公式，然后把P点的坐标代入椭圆方程利用基本不等式求面积的最小值．
解答： 解：（1）∵
OA
=（2
2
，0），且
OB
+
OA
=
0
，
∴
OB
=-
OA
=(-2
2
，0)，
又|
BE
-
BA
|+|
AE
-
AB
|=6，即|
AE
|+|
BE
|=6．
∴动点E的轨迹为以B，A为焦点，6为长轴的椭圆，
由2a=6，a=3，c=2
2
，
∴b2=a2-c2=9-8=1．
∴动点E的轨迹方程C：
x2
9
+y2=1；
（2）设点P（x0，y0），则以|OP|为直径的圆的方程为x2-x0x+y2-y0y=0．
与圆的方程x2+y2=1相减得：x0x+y0y=1，此方程即是过切点A，B的直线方程（x0y0≠0）．
令x=0，得y=
1
y0
，∴N（0，
1
y0
）；
令y=0，得x=
1
x0
，∴M（
1
x0
，0）．
∴|MN|=
(
1
x0
)2+(
1
y0
)2
=
x02+y02
|x0y0|
，
点O到直线MN的距离d=
1
x02+y02
，
∴S△OMN=
1
2
d|MN|=
1
2
•
1
|x0y0|
，
∵点P在椭圆C：
x2
9
+y2=1上，
∴1=
x02
9
+y02≥2
x02y02
9
=
2|x0y0|
3
，
当|x0|=|3y0|时取等号．
∴2|x0y0|≤3，
∴S△OMN≥
1
2
×
2
3
=
1
3
．
故△MON面积的最小值是
1
3
．
点评：本题是直线与圆锥曲线的综合题，考查了椭圆方程的求法，训练了由圆系方程求过圆的两切点的直线方程的方法，考查了利用基本不等式求函数最值，属难题．
练习册系列答案
相关题目
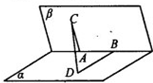如图，在二面角α-AB-β的棱上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直于AB，已知AB=4，AC=6，BD=8，CD=2
17
，则直线CD与平面α所成角的正弦值为（　　）
A、
697
34
B、
3
51
64
C、
697
64
D、
3
51
34
已知椭圆Γ的中心在原点，焦点在x轴上，离心率为
3
2
，且过抛物线C：x2=4y的焦点F．
（1）求椭圆Γ的方程；
（2）设点F关于x轴的对称点为F′，过F′作两条直线l1和l2，其斜率分别为k、k′，满足k＞0，k+k′=0，它们分别是椭圆Γ的上半部分相交于G，H两点，与x轴相交于A，B两点，使得|GH|=
16
5
，求证：△ABF′的外接圆过点F；
（3）设抛物线C的准线为l，P，Q是抛物线上的两个动点，且满足∠PFQ=
π
2
，线段PQ的中点为M，点M在l上的投影为N，求
|MN|
|PQ|
的最大值．
已知点A（-1，0）、B（1，0），直线AM与BM相交于点M，且它们的斜率之积为-2，
（1）求动点M的轨迹E的方程；
（2）若过点N（
1
2
，1）的直线l交动点M的轨迹于C、D两点，且点N为CD的中点，求直线l的方程．
设集合M={a，b}，N={c，d}，定义M与N的一个运算“•”为：M•N={x|x=mn，m∈M，n∈N}．
（1）对于交集，有性质A∩B=B∩A；类比以上结论是否有M•N=N•M？并证明你的结论．
（2）举例验证（A•B）•C=A•（B•C）．
设两圆C1：（x-
2
）2+y2=1和C2：x2+y2+2
2
x=0的圆心分别为C1、C2，G1、G2分别是圆C1、C2上的点，M是动点，且|MC1|+|MC2|=4
（1）求动点M的轨迹L的方程；
（2）设轨迹H与y轴的一个交点为B（0，-b），是否存在直线l：y=x+m，使点B关于直线l的对称点落在轨迹L上，若存在，求出直线l的方程，若不存在，请说明理由．
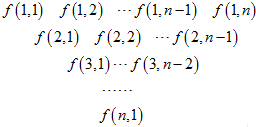一个三角形数表按如下方式构成（如图：其中项数n≥5）：第一行是以4为首项，4为公差的等差数列，从第二行起，每一个数是其肩上两个数的和，例如：f（2，1）=f（1，1）+f（1，2）；f（i，j）为数表中第i行的第j个数．
（1）求第2行和第3行的通项公式f（2，j）和f（3，j）；
（2）证明：数表中除最后2行外每一行的数都依次成等差数列，并求f（i，1）关于i（i=1，2，…，n）的表达式；
（3）若f（i，1）=（i+1）（ai-1），bi=
1
aiai+1
，试求一个等比数列g（i）（i=1，2，…，n），使得Sn=b1g（1）+b22g（2）+…+bng（n）＜
1
3
，且对于任意的m∈（
1
4
，
1
3
）均存在实数λ，当n＞λ时，都有Sn＞m．
在椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0），中，F1，F2分别为左右焦点A1，A2，B1，B2分别为四个顶点，已知菱形A1B1A2B2和菱形B1F1B2F2的面个积分别为4
3
和2
3
．
（1）求椭圆C的标准方程；
（2）过椭圆C的右顶点A2作两条互相垂直的直线分别和椭圆交于另一点P，Q，试判断直线PQ是否过定点，若过定点，求出该定点的坐标；若不过定点，请说明理由．
已知椭圆C的两个焦点分别为F1（-
3
，0），F2（
3
，0），短轴的两个端点分别为B1，B2；且△F1B1B2为等腰直角三角形．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若直线l与椭圆C交于点M，N，且OM⊥ON，试证明直线l与圆x2+y2=2相切．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网