题目内容

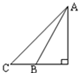如图，在高为20m的楼顶A处观察前下方一座横跨河流的桥BC，测得桥两端B，C的俯角分别为60°，45°，则桥的长度为（　　）
A、
20
3
3
m
B、10
3
m
C、20-
20
3
3
m
D、20-10
3
m
考点：解三角形的实际应用
专题：计算题,解三角形
分析：设垂足为D，则tan60°=
20
BD
，tan45°=
20
CD
，求出BD，CD，可得桥的长度．
解答： 解：设垂足为D，则tan60°=
20
BD
，tan45°=
20
CD
，
∴BD=
20
3
3
m，CD=20，
∴BC=（20-
20
3
3
）m，
故选：C．
点评：本题考查解三角形的实际应用，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
复数 z=x+yi（x，y∈R）满足方程|z-1|=2|z|，则在复平面上表示复数z的动点Z的轨迹图形是（　　）
A、直线B、圆C、椭圆D、抛物线
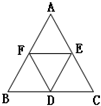
D、E、F分别是△ABC三边BC、CA、AB中点，则
DE
+
EF
+
DF
=（　　）
A、-
AC
B、-
1
2
AC
C、
AC
D、
O
曲线y=ax2+2lnx有平行于x轴的切线，则实数a的取值范围为
 
．
抛物线y2=8x上一点P到其焦点的距离为9，则其横坐标为
 
．
二进制数10000001001转化为八进制数是
 
．
设f0（x）=sinx，f1（x）=f0′（x），f2（x）=f1′（x），…，fn+1（x）=fn′（x），n∈N，则f2005（x）=
 
．
经过点（-1，1），倾斜角是直线y=
2
2
x-2的倾斜角的2倍的直线方程是（　　）
A、x=-1
B、y=1
C、y-1=
2
（x+1）
D、y-1=2
2
（x+1）
在数列{an}中，a1=4，an+1=f（an），且f（x）满足下表，则a2013=（　　）
x12345
f（x）54213
A、2B、4C、5D、3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网