题目内容
复数 z=x+yi（x，y∈R）满足方程|z-1|=2|z|，则在复平面上表示复数z的动点Z的轨迹图形是（ ）
| A、直线 | B、圆 | C、椭圆 | D、抛物线 |
考点：轨迹方程,复数求模
专题：计算题,直线与圆
分析：由题意把|z-1|=2|z|平方可得关于x、y的方程，化简方程可判其对应的图形．
解答：
解：∵z=x+yi，|z-1|=2|z|，
∴|z-1|2=（2|z|）2，
∴|x-1+yi|2=（2|x+yi|）2，
∴（x-1）2+y2=4（x2+y2），
化简可得3x2+3y2+2x-1=0，
可得22+02-4×3×（-1）=16＞0，
故该方程表示的图形为圆，
故选：B．
∴|z-1|2=（2|z|）2，
∴|x-1+yi|2=（2|x+yi|）2，
∴（x-1）2+y2=4（x2+y2），
化简可得3x2+3y2+2x-1=0，
可得22+02-4×3×（-1）=16＞0，
故该方程表示的图形为圆，
故选：B．
点评：本题考查复数的代数形式及其几何意义，考查圆的方程，涉及复数的模长公式，属基础题．
练习册系列答案
相关题目
程序框图是算法思想的重要表现形式，程序框图中不含（ ）
| A、流程线 | B、判断框 |
| C、循环框 | D、执行框 |
将y=f′（x）sinx图象向左平移
个单位，得y=1-2sin2x图象，则f（x）=（ ）
| π |
| 4 |
| A、2cosx | B、2sinx |
| C、sinx | D、cosx |
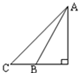如图，在高为20m的楼顶A处观察前下方一座横跨河流的桥BC，测得桥两端B，C的俯角分别为60°，45°，则桥的长度为（ ）A、
| ||||
B、10
| ||||
C、20-
| ||||
D、20-10
|