题目内容
曲线y=ax2+2lnx有平行于x轴的切线,则实数a的取值范围为 .
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:求出原函数的导函数,由曲线y=ax2+2lnx存在平行于x轴的切线得导函数对应的方程有解,由此求得a的范围.
解答:
解:由y=ax2+2lnx,得y′=2ax+
,
若曲线y=ax2+2lnx存在平行于x轴的切线,
则y′=2ax+
=0(x>0)有解,
即x2=-
>0,a<0.
∴实数a的取值范围是(-∞,0).
故答案为:(-∞,0).
| 2 |
| x |
若曲线y=ax2+2lnx存在平行于x轴的切线,
则y′=2ax+
| 2 |
| x |
即x2=-
| 1 |
| a |
∴实数a的取值范围是(-∞,0).
故答案为:(-∞,0).
点评:本题考查了利用导数研究过曲线上某点处的切线方程,考查了数学转化思想方法,是中档题.

练习册系列答案
相关题目
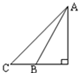 如图,在高为20m的楼顶A处观察前下方一座横跨河流的桥BC,测得桥两端B,C的俯角分别为60°,45°,则桥的长度为( )
如图,在高为20m的楼顶A处观察前下方一座横跨河流的桥BC,测得桥两端B,C的俯角分别为60°,45°,则桥的长度为( )A、
| ||||
B、10
| ||||
C、20-
| ||||
D、20-10
|