题目内容
在数列{an}中，a1=4，an+1=f（an），且f（x）满足下表，则a2013=（ ）
| x | 1 | 2 | 3 | 4 | 5 |
| f（x） | 5 | 4 | 2 | 1 | 3 |
| A、2 | B、4 | C、5 | D、3 |
考点：数列递推式
专题：等差数列与等比数列
分析：由已知条件推导出数列的前6项，得{an}是以5为周期的周期数列，由此能求出a2013=a3=5．
解答：
解：∵a1=4，an+1=f（an），
∴由题意知a2=f（4）=1，
a3=f（1）=5，
a4=f（5）=3，
a5=f（3）=2，
a6=f（2）=4，
∴{an}是以5为周期的周期数列，
∵2013=402×5+3，
∴a2013=a3=5．
故答案为：5．
∴由题意知a2=f（4）=1，
a3=f（1）=5，
a4=f（5）=3，
a5=f（3）=2，
a6=f（2）=4，
∴{an}是以5为周期的周期数列，
∵2013=402×5+3，
∴a2013=a3=5．
故答案为：5．
点评：本题考查数列的第2013项的求法，是基础题，解题时要注意数列的周期性的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
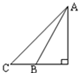如图，在高为20m的楼顶A处观察前下方一座横跨河流的桥BC，测得桥两端B，C的俯角分别为60°，45°，则桥的长度为（ ）A、
| ||||
B、10
| ||||
C、20-
| ||||
D、20-10
|
如图，在正方体ABCD-A1B1C1D1中，E为AB中点，设I为全集，集合M，N，P都是其子集，则图中的阴影部分表示的集合为（ ）
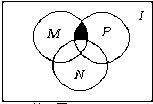
| A、M∩（N∪P） |
| B、M∩（P∩∁IN） |
| C、P∩（∁IN∩∁IM ） |
| D、（M∩N）∪（M∩P） |
在等差数列{an}中，a1=3，a3=4，则a5=（ ）
| A、3 | B、4 | C、5 | D、-1 |
在等比数列{an}中，a1=
，a4=
，则数列的公比q为（ ）
| 1 |
| 2 |
| 1 |
| 16 |
A、
| ||
B、±
| ||
C、
| ||
D、±
|
已知函数y=f（x）的定义域是[-1，4]，则y=f（2x-1）的定义域是（ ）
A、[0，
| ||
| B、[-1，4] | ||
| C、[-5，5] | ||
| D、[-3，7] |