题目内容
设f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N,则f2005(x)= .
考点:导数的运算
专题:导数的概念及应用
分析:通过计算前几项,进行归纳分析,当计算到f4(x)时发现f4(x)=f0(x),所以可看成以4为一个循环周期,那么f2005(x)=f1(x)=cosx
解答:
解:∵f0(x)=sinx,
∴f1(x)=f0′(x)=cosx,
∴f2(x)=f1′(x)=-sinx,
∴f3(x)=f2′(x)=-cosx,
∴f4(x)=f3′(x)=sinx,
…
由引可以得出呈周期为4的规律重复出现,
∵2005=4×501+1
则f2005(x)=f1(x)=cosx,
故答案为:cosx
∴f1(x)=f0′(x)=cosx,
∴f2(x)=f1′(x)=-sinx,
∴f3(x)=f2′(x)=-cosx,
∴f4(x)=f3′(x)=sinx,
…
由引可以得出呈周期为4的规律重复出现,
∵2005=4×501+1
则f2005(x)=f1(x)=cosx,
故答案为:cosx
点评:本题考查导数的运算,求解本题的关键是掌握正、余弦函数的求导公式,以及在求导过程中找出解析式变化的规律,归纳总结是解题过程中发现规律的好方式.本题考查了归纳推理.

练习册系列答案
相关题目
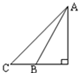 如图,在高为20m的楼顶A处观察前下方一座横跨河流的桥BC,测得桥两端B,C的俯角分别为60°,45°,则桥的长度为( )
如图,在高为20m的楼顶A处观察前下方一座横跨河流的桥BC,测得桥两端B,C的俯角分别为60°,45°,则桥的长度为( )A、
| ||||
B、10
| ||||
C、20-
| ||||
D、20-10
|
当λ变化时,直线λx-y+2+λ=0经过的定点是( )
| A、(1,2) |
| B、(-1,2) |
| C、(1,-2) |
| D、(-1,-2) |
在等比数列{an}中,a1=
,a4=
,则数列的公比q为( )
| 1 |
| 2 |
| 1 |
| 16 |
A、
| ||
B、±
| ||
C、
| ||
D、±
|

 如图,在正方体ABCD-A1B1C1D1中,E为AB中点,
如图,在正方体ABCD-A1B1C1D1中,E为AB中点,