题目内容
经过点(-1,1),倾斜角是直线y=
x-2的倾斜角的2倍的直线方程是( )
| ||
| 2 |
| A、x=-1 | ||
| B、y=1 | ||
C、y-1=
| ||
D、y-1=2
|
考点:二倍角的正切,直线的斜率
专题:直线与圆
分析:先求出直线的倾斜角,再用点斜式求得直线的方程.
解答:
解:直线y=
x-2的倾斜角为α,tanα=
,
经过点(-1,1),倾斜角是直线y=
x-2的倾斜角的2倍的直线的倾斜角为2α,
∴直线的斜率K=
=
=2
再根据直线经过点(-2,1),可得直线的方程为 y-1=2
(x+1),
故选:D.
| ||
| 2 |
| ||
| 2 |
经过点(-1,1),倾斜角是直线y=
| ||
| 2 |
∴直线的斜率K=
| 2tanα |
| 1-tan2α |
2×
| ||||
1-
|
| 2 |
再根据直线经过点(-2,1),可得直线的方程为 y-1=2
| 2 |
故选:D.
点评:本题主要考查直线的倾斜角和斜率的关系,用点斜式求直线的方程,属于基础题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
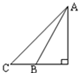 如图,在高为20m的楼顶A处观察前下方一座横跨河流的桥BC,测得桥两端B,C的俯角分别为60°,45°,则桥的长度为( )
如图,在高为20m的楼顶A处观察前下方一座横跨河流的桥BC,测得桥两端B,C的俯角分别为60°,45°,则桥的长度为( )A、
| ||||
B、10
| ||||
C、20-
| ||||
D、20-10
|
当λ变化时,直线λx-y+2+λ=0经过的定点是( )
| A、(1,2) |
| B、(-1,2) |
| C、(1,-2) |
| D、(-1,-2) |
已知等比数列{an}满足an>0,n=1,2,…,且a5•a2n-5=22n(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n-1=( )
| A、n(2n-1) |
| B、(n+1)2 |
| C、n2 |
| D、(n-1)2 |
已知函数y=f(x)的定义域是[-1,4],则y=f(2x-1)的定义域是( )
A、[0,
| ||
| B、[-1,4] | ||
| C、[-5,5] | ||
| D、[-3,7] |
 如图,在正方体ABCD-A1B1C1D1中,E为AB中点,
如图,在正方体ABCD-A1B1C1D1中,E为AB中点,