题目内容

二进制数10000001001转化为八进制数是
 
．
考点：进位制
专题：算法和程序框图
分析：由二进制转化为十进制的方法，我们只要依次累加各位数字上的数×该数位的权重，即可得到十进制数，再利用“除k取余法”是将十进制数除以8，然后将商继续除以8，直到商为0，然后将依次所得的余数倒序排列即可得到答案．
解答： 解：10000001001（2）=1×20+1×23+1×210=1033，
1033÷8=129…1
129÷8=16…1
16÷8=2…0
2÷8=0…2
故1029（10）=2011（8）
故答案为：2011．
点评：本题考查的知识点是算法的概念，由二进制转化为八进制的方法，进制转换为十进制的方法是依次累加各位数字上的数×该数位的权重，十进制与其它进制之间的转化，熟练掌握“除k取余法”的方法步骤是解答本题的关键．
练习册系列答案
相关题目
对于函数y=x2，其导数等于原来函数值的点是
 
．
不等式
x-2
x2-2x-3
≤0的解集为
 
．
已知A={x|x2-6x+8≤0}，B={x|
2
x-1
≥0}，C={x|x2-mx+6＜0}且“x∈A∩B”是“x∈C”的充分不必要条件，求实数m的取值范围．
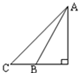如图，在高为20m的楼顶A处观察前下方一座横跨河流的桥BC，测得桥两端B，C的俯角分别为60°，45°，则桥的长度为（　　）
A、
20
3
3
m
B、10
3
m
C、20-
20
3
3
m
D、20-10
3
m
假设每一架飞机的引擎在飞行中出现故障率为1-p，且各引擎是否有故障是独立的，如有至少50%的引擎能正常运行，飞机就可成功飞行，若使4引擎飞机比2引擎飞机更为安全，则p的取值范围是（　　）
A、（
2
3
，1）
B、（
1
3
，1）
C、（0，
1
4
）
D、（0，
2
3
）
y=e3的导数是
 
．
已知等比数列{an}满足an＞0，n=1，2，…，且a5•a2n-5=22n（n≥3），则当n≥1时，log2a1+log2a3+…+log2a2n-1=（　　）
A、n（2n-1）
B、（n+1）2
C、n2
D、（n-1）2
在等差数列{an}中，a1=3，a3=4，则a5=（　　）
A、3B、4C、5D、-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网