题目内容

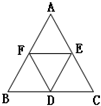
D、E、F分别是△ABC三边BC、CA、AB中点，则
DE
+
EF
+
DF
=（　　）
A、-
AC
B、-
1
2
AC
C、
AC
D、
O
考点：向量的加法及其几何意义
专题：平面向量及应用
分析：利用三角形的中位线定理、向量的三角形法则及其共线定理即可得出．
解答： 解：∵D、E、F分别是△ABC三边BC、CA、AB中点，
∴
AC
=2
FD
．
∴
DE
+
EF
+
DF
=2
DF
=-
AC
．
故选：A．
点评：本题考查了三角形的中位线定理、向量的三角形法则及其共线定理，属于基础题．
练习册系列答案
相关题目
将y=f′（x）sinx图象向左平移
π
4
个单位，得y=1-2sin2x图象，则f（x）=（　　）
A、2cosxB、2sinx
C、sinxD、cosx
某几何体的三视图如图所示，则该几何体的体积为
 
．
sin165°=
 
．
有一段“三段论”推理：对于可导函数f（x），若f（x）在区间（a，b）上是增函数，则f′（x）＞0对x∈（a，b）恒成立，因为函数f（x）=x3在R上是增函数，所以f（x）=3x2＞0对x∈R恒成立．以上推理中（　　）
A、大前提错误
B、小前提错误
C、推理形式错误
D、推理正确
不等式
x-2
x2-2x-3
≤0的解集为
 
．
下列计算正确的有（　　）个
①（-7）×6
a
=-42
a
；②（
a
-2
b
）+2
a
+2
b
=3
a
；③（
a
+
b
）-（
a
-
b
）=0．
A、0B、1C、2D、3
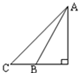如图，在高为20m的楼顶A处观察前下方一座横跨河流的桥BC，测得桥两端B，C的俯角分别为60°，45°，则桥的长度为（　　）
A、
20
3
3
m
B、10
3
m
C、20-
20
3
3
m
D、20-10
3
m
如图，在正方体ABCD-A1B1C1D1中，E为AB中点，
（1）求证：AD1⊥平面CDA1B1；
（2）求异面直线C1E与AA1所成的角的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网