题目内容
9.已知数列{an}满足:a1=3,an+1=9•$\root{3}{{a}_{n}}$(n≥1),则$\underset{lim}{n→∞}$an=27.分析 把已知数列递推式两边取常用对数,然后构造等比数列,求出数列{an}的通项公式,则极限可求.
解答 解:由an+1=9•$\root{3}{{a}_{n}}$(n≥1),得$lg{a}_{n+1}=lg9+lg\root{3}{{a}_{n}}$,
即$lg{a}_{n+1}=\frac{1}{3}lg{a}_{n}+2lg3$,令bn=lgan,
则${b}_{n+1}=\frac{1}{3}{b}_{n}+2lg3$,∴${b}_{n+1}-3lg3=\frac{1}{3}({b}_{n}-3lg3)$,
则数列{bn-3lg3}是以b1-3lg3=lga1-3lg3=-2lg3为首项,以$\frac{1}{3}$为公比的等比数列,
∴${b}_{n}-3lg3=-2lg3•(\frac{1}{3})^{n-1}$,即${b}_{n}=3lg3-2lg3•(\frac{1}{3})^{n-1}$,
∴${a}_{n}=1{0}^{3lg3-2lg3•(\frac{1}{3})^{n-1}}$,
则$\underset{lim}{n→∞}$an=$\underset{lim}{n→∞}1{0}^{3lg3-2lg3•(\frac{1}{3})^{n-1}}$=103lg3=10lg27=27.
故答案为:27.
点评 本题考查数列极限的求法,考查了构造等比数列的方法,训练了等比数列通项公式的求法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.已知向量$\overrightarrow{a}$=(2cosφ,2sinφ),φ∈(90°,180°),$\overrightarrow{b}$=(1,1),则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | φ | B. | 45°+φ | C. | 135°-φ | D. | φ-45° |
17.定义在(0,+∞)上的可导函数f(x)满足:当x∈(0,e)时f(x)+xf′(x)>$\frac{1}{e}$当x∈(e,+∞)时f(x)+xf′(x)<$\frac{1}{e}$则下列对于2f(2),3f(3)大小关系的结论成立的是( )
| A. | 2f(2)>3f(3) | B. | 2f(2)<3f(3) | C. | 2f(2)=3f(3) | D. | 无法确定 |
14.已知如图所示的程序框图,当输入n=99时,输出S的值( )
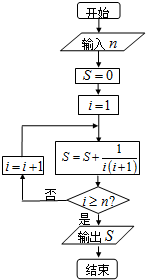

| A. | $\frac{100}{101}$ | B. | $\frac{99}{100}$ | C. | $\frac{98}{99}$ | D. | $\frac{97}{98}$ |
18.仔细观察下面○和●的排列规律:○●○○●○○○●○○○○●○○○○○●○○○○○○●…
若依此规律继续下去,得到一系列的○和●,那么在前150个○和●中,●的个数是( )
若依此规律继续下去,得到一系列的○和●,那么在前150个○和●中,●的个数是( )
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
19.如图,在直角坐标系内,射线OT落在60°的终边上,任作一条射线OA,则射线落在∠xOT内的概率是( )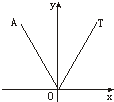

| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | 以上全不对 |
 如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,点D是AB的中点.
如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,点D是AB的中点.