题目内容
19.如图,在直角坐标系内,射线OT落在60°的终边上,任作一条射线OA,则射线落在∠xOT内的概率是( )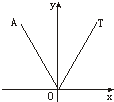
| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | 以上全不对 |
分析 根据周角等于360°,得到所有的基本事件对应的图形是360°角的整个平面区域,再根据射线OT落在60°的终边上,得到符合题意的事件对应的图形是所成角为60°的两条射线之间区域.最后用符合题意的图形对应的角度,除以所有的基本事件对应图形的角度,可得OA落在∠xOT内的概率.
解答 解:∵周角等于360°,
∴任作一条射线OA,它的运动轨迹可以绕原点旋转一周,
所以所有的基本事件对应的图形是360°角的整个平面区域.
∵射线OT落在60°的终边上,
∴若OA落在∠xOT内,符合题意的事件对应的图形是所成角为60°的两条射线之间区域,
记事件X=“任作一条射线OA,OA落在∠xOT内”,
可得所求的概率为:P(x)=$\frac{60}{360}$=$\frac{1}{6}$.
故选:A.
点评 本题以作一条射线,求落在指定区域的事件概率为载体,着重考查了用几何图形求概率的知识,属于基础题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
7.设函数f(x)=$\left\{{\begin{array}{l}{1+{{log}_2}({2-x}),x<1}\\{{2^{x-1}},x≥1}\end{array}}$,则f(-6)+f(log212)=( )
| A. | 10 | B. | 6 | C. | 9 | D. | 12 |
4.cos1050°=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
3.设集合A={x|x2+2x-3>0},B={x|x2-2ax-1≤0,a>0},若A∩B中恰有一个整数,则实数a的取值范围是( )
| A. | (0,$\frac{3}{4}$) | B. | [$\frac{3}{4}$,$\frac{4}{3}$) | C. | $[\frac{3}{4},+∞)$ | D. | (1,+∞) |